mechanika45

Rozwiązanie

Przy ciężarze C^, s G ś G_nux układ pozostaje w równowadze statycznej.

^a) G = Gmia

Przy G < G_młn nastąpi ruch ciała Q w lewo, a więc zwrot siły tarcia T nale ży przyjąć w prawo. Myślowo przecinamy linę w punktach styku z ciałami sztywnymi i ujawniamy naciągi w poszczególnych odcinkach prostoliniowych Schemat obliczeniowy ma postać:

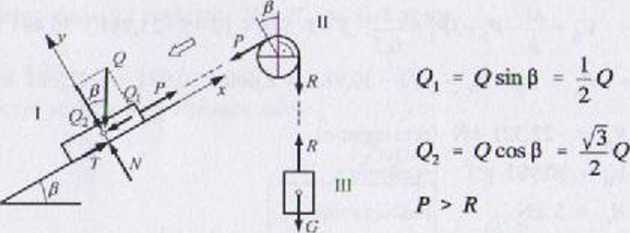
X

^VL

W celu wyznaczenia zależności między Q i G można rozpatrywać podukłady w kolejności I. II. III lub III. U, I. Zadanie łatwiej rozwiązać przyjmując kolejność III. II. I.

Podukład III: 1RRS

£ Z = 0: R-G - 0 =» R = G

Podukład II (cięgno przełożone przez krążek):

a = 90" +30” = 120° = 120"*    ⁷¹    = -it rad (kąt opasania i

180°    3

(!)

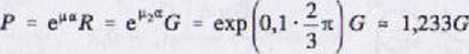
(2)

Podukład I: 2RRS £ * - 0: P + T <?, = 0 £ Y = 0: N Q₇ = 0

‘>0

Statyka. 1.2. \ Równowaga granic/n.i mechanizmów płaskich / tarciem

0! n = Q₇ = <?cosp ~^Q, T = \iN = p, N »0,2• Q = 0 J v/3G (|i «=> P = Q_}-T

1,233G = tfsinP - OJ ^C?

1,2330 -    - OJ v/3 (? =» U33G = 0.327G |: 1,233

G = C_min = 0,265(? - 0,265 • 2000 = 530 N

!''/'• G > G^ nastąpi ruch ciała Q w prawo, a więc zwrot siły tarcia T pilr/y przyjąć w lewo. Myślowi) przecinamy linę w punktach styku z ciałami tltywnyrai i ujawniamy naciągi P_y R.

\ liemat obliczeniowy ma postać:

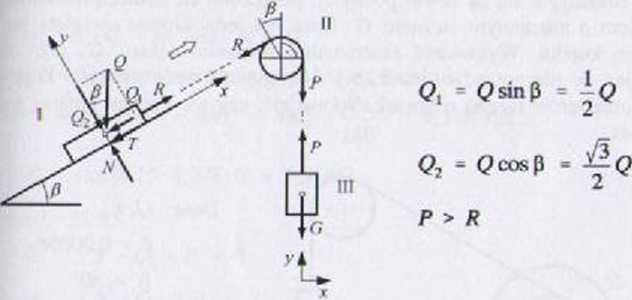
r.Kiukład III: 1RRS >;y^/ = 0: /* - G = 0 —» P = G

Podukład II (cięgno przełożone przez krążek):

2

a - k rad (kąt opasania - jak w przypadku G^)

N e^P = t**G * ex_P[-0,l|n|G = 0.811G Podukład I: 2RRS

£< - 0: R Q, T = 0    (I)

£ V - 0: N -Q₂ = 0    (2)

91

Si.iiyka. 1.2. i Równowaga gr.uik/nu mcchumzmów płaskich / lurdcm