mechanika7

Dwa układy obciążeń są sobie równoważne, jeśli zastąpienie jednego układu obciążeń układem drugim wywołuje takie same skutki. Redukcją układu obciążeń nazywamy zastąpienie tego układu najprostszym układem równoważnym.

Układ obciążeń działających na ciało sztywne jest w równowadze statycznej. jeśli redukuje się do zera.

Statyka jest działem mechaniki ogólnej zajmującym się badaniem równowagi statycznej układów obciążeń i przekształcaniem tych układów.

Prawa Newtona

I: Jeśli układ sił działających na punkt materialny jest w równowadze statycznej, to punkt ten jest nieruchomy lub jest w ruchu prostoliniowym jednostajnym.

II: Pochodna pędu punktu materialnego jest równa sile działającej na len punkt¹.

III Dwa punkty materialne przyciągają się z silą grawitacji (rys. 1.1 Oa):

P « k ^ml^rh_t = 6,67• 10"¹ r⁷

(1.21)

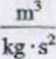
gdzie: m,, m₂ — masy punktów materialnych,

r — odległość punktów materialnych, k - stała grawitacji.

W warunkach ziemskich prawo grawitacji objawia się siłą ciężkości punktu materialnego (rys. 1.1 Ob)

(1.22)

G = //ig, g = 9,81 “

s^Ł

gdzie g jest przyspieszeniem ziemskim.

b)

p

Rys. 1.10

|V Jeśli ciało A działa na ciało B silą R, lo ciało B działa na ciało A siłą kolincamą -R, rys. 1.11.

Siły R. -R mają jednakową wartość, wspólną prostą działania i przeciwne zwroty.

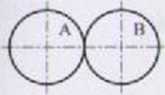
Rys. 1.11

\lvsjomaty statyki

i I >wie siły kolineame. o tej samej wartości i przeciwnych zwrotach są w równowadze statycznej (rys. 1.12). Układ taki nazywamy ..układem zerowym sil”

*    ^r    U

A

Rys. 1.12

¹ Parę sił działającą w płaszczyźnie xy można zastąpić momentem M = Pa, który jest wektorem swobodnym, o zwrocie zgodnym z. regułą prawej dłoni, prostopadłym do płaszczyzny xy (rys. 1.13). Moment ten nazywamy „momentem pary sił".

a)    b)

i	y			y
	p		P	p
A#				JU
		-JUL			sJL

⁴

U_s = kh*Pa

Rys. 1.13

' Dwie siły zbiezne (tzn. o prostych działania przecinających się) działające na punkt A można zastąpić wypadkową, będącą przekątną równoleglobo-ku „rozpiętego” na tych siłach (rys. 1.14).

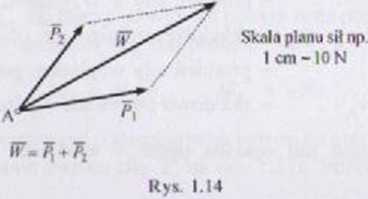
Stniykn Kalunwy Uur.iyi mc 15

1

prawo Newtona zmianie szczegółowo omówione w rozdziale 3.