Metoda Gaussa Jordana

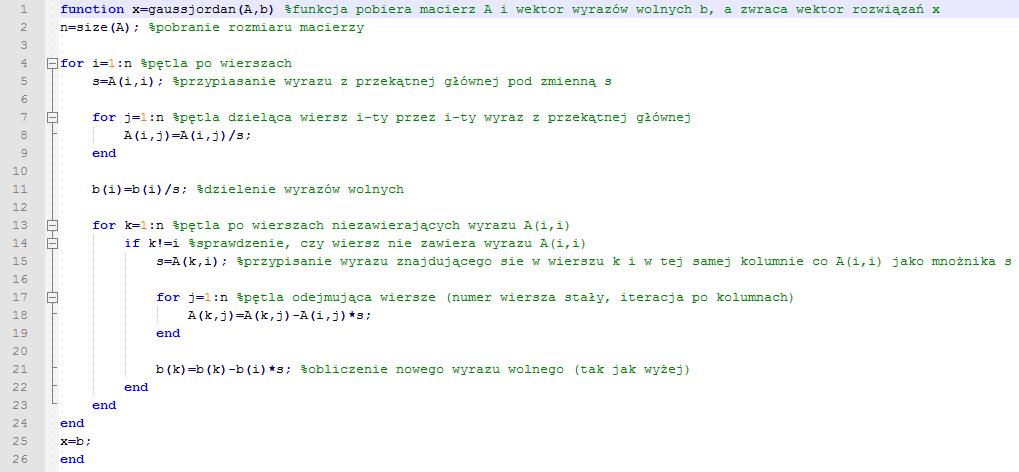
function x=gaussjordan(A,b) %funJccja pobiera macierz A i wektor wyrazów wolnych b, a zwraca wektor rozwiązań x n=size(A); %pobranie rozmiaru macierzy

F)for i= :n %pętla po wierszach

s=A(i,i); %przypiasanie wyrazu z przekątnej głównej pod zmienną s

E3 for j= :n %pętla dzieląca wiersz i-ty przez i-ty wyraz z przekątnej głównej A(i/j)=A(i,j)/s;

end

b(i)=b(i)/s; %dzielenie wyrazów wolnych

-UHD-

for k=l:n %pętla po wierszach niezawierających wyrazu A(i,i)

if k!=i %sprawdzenie, czy wiersz nie zawiera wyrazu A(i,i)

s=A(k,i); %przypisanie wyrazu znajdującego sie w wierszu k i w tej samej kolumnie co A(i,i) jako mnożnika s

0    for j=l:n %pętla odejmująca wiersze (numer wiersza stały, iteracja po kolumnach)

A (k, j ) =A (k, j ) -A (i, j ) *s ;

end b(k)=b(k)-b(i)*s; %obliczenie nowego wyrazu wolnego (tak jak wyżej)

end

end

end x=b; end