Metoda Gradientów Sprzężonych

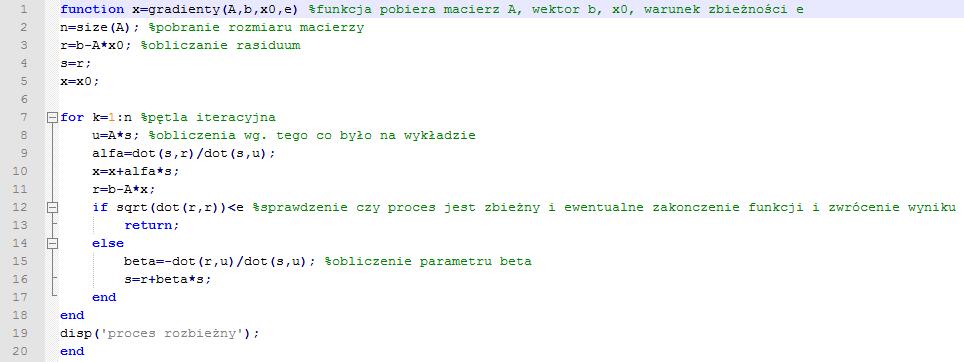
function x=gradienty(A,b,xQ,e) %funkcja pobiera macierz A, wektor b, xQ, warunek zbieżności e

n=size(A); %pobranie rozmiaru macierzy

r=b-A*xO; %obliczanie rasiduum

s=r;

x=x0 ;

Rfor k= :n %pętla iteracyjna

u=A*s; %obliczenia wg. tego co było na wykładzie alfa=dot(s,r)/dot(s,u); x=x+alfa*s; r=b-A*x;

if sqrt(dot(r,r))<e %sprawdzenie czy proces jest zbieżny i ewentualne zakończenie funkcji i zwrócenie wyniku return;

else

beta=-dot(r,u)/dot(s,u); %obliczenie parametru beta s=r+beta*s;

end

end

disp('proces rozbieżny'); end