Metoda Gaussa Seidla

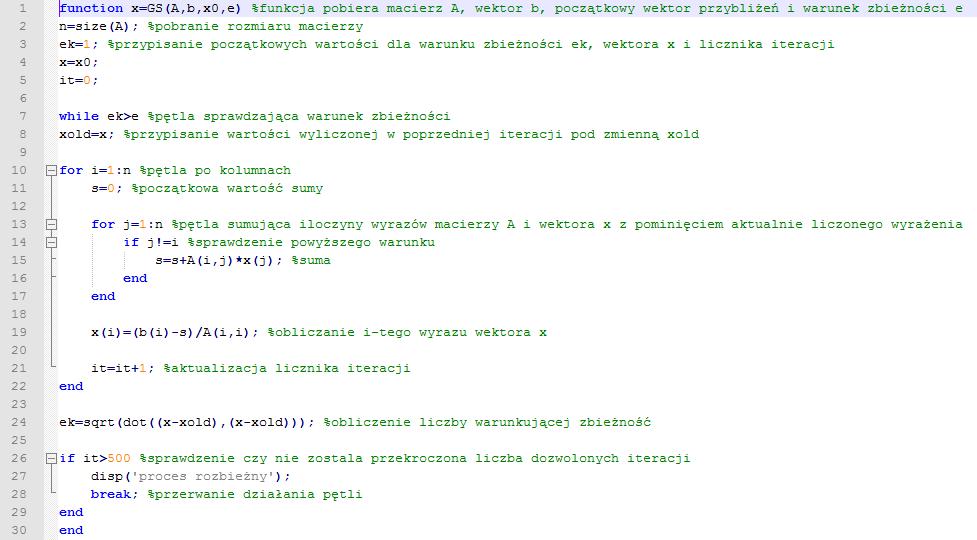
(function x=GS(A,b,xO,e) %funkcja pobiera macierz A, wektor b, początkowy wektor przybliżeń i warunek zbieżności e n=size(A); %pcbranie rozmiaru macierzy

ek=l; %przypisanie początkowych wartości dla warunku zbieżności ek, wektora x i licznika iteracji x=x0 ; it=0;

while ek>e %pętla sprawdzająca warunek zbieżności

xold=x; %przypisanie wartości wyliczonej w poprzedniej iteracji pod zmienną xold

Tfor i=I:n %pętla po kolumnach

s=0; %początkowa wartość sumy

for j=l:n %pętla sumująca iloczyny wyrazów macierzy A i wektora x z pominięciem aktualnie liczonego wyrażenia if j!=i %sprawdzenie pcv;yższegc warunku s=s+A(i,j)*x(j); %suma

end

end

x(i)=(b(i)-s)/A(i,i); %obliczanie i-tego wyrazu wektora x it=it+l; %aktualizacja licznika iteracji

end

ek=3qrt(dot((x-xold),(x-xold))); %obliczenie liczby warunkującej zbieżność

if it>500 %sprawdzenie czy nie zestala przekroczona liczba dozwolonych iteracji disp('proces rozbieżny’); break; %przerwanie działania pętli

end

end