P6063267

kolejnych stanów naprężenia w układzie współrzędnych t_/f jak też nanosząc tylko położenia punktów o maksymalnej wartości naprężenia ścinającego w układzie q_y p, Rycina 47b przedstawia kolejne stany naprężeń: od wszechstronnego hydrostatycznego ściskania (punkty 1 i 6), przez kolejne zwiększanie naprężenia głównego <7, (dla pierwszej próbki koła 2, 3, 4) i zmniejszanie <r₃ (koło 5 dla pierwszej próbki i koła 7, 8, 9 dla drugiej próbki). l inia łączącą te punkty obrazuje przebieg stanu

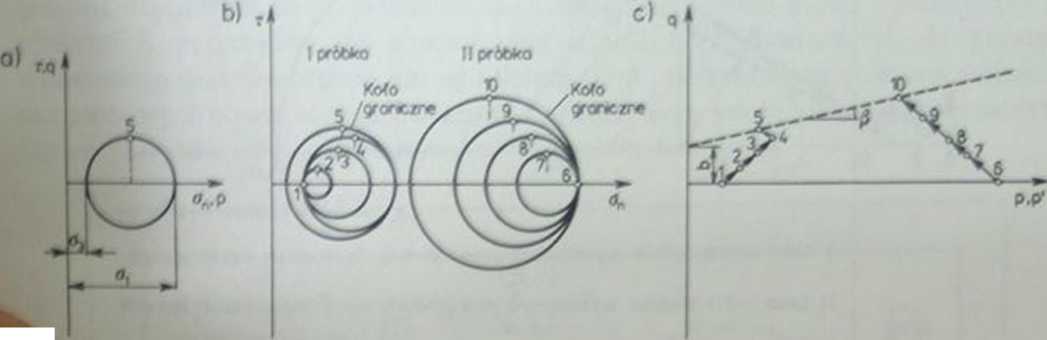
Ryc. 47. Ścieżka obciążeń

naprężenia i nazywamy ją ścieżką obciążenia (ryc. 47c). Ścieżkę obciążenia można zdefiniować jako zbiór punktów o maksymalnym naprężeniu ścinającym, jakie występuje w rozpatrywanym elemencie gruntu w przypadku zmiany wywieranych obciążeń, ł ącząc końcowe punkty ścieżki obciążeń dla kilku próbek tego samego gruntu otrzymuje się linie wytrzymałości na ścinanie w układzie q = q\ p (lub q\ p').

Związek pomiędzy liniami wytrzymałości na ścinanie określonymi przez punkty styczności o współrzędnych r_/f n_n (1) i przez punkty o współrzędnych q_y p (II) przedstawia rycina 48. Jak wynika z tej ryciny, warunek ścięcia próbki można określić analitycznie na podstawie wzoru:

~ff₃ = 2ccos0 + (ff_l +<r₃)sintf>

lub w postaci:

0,5(<7, -<t₃) = Z> + 0,5(<7, +<7₃)tg//

Z powyższych danych wynika, że linia wytrzymałości I nie jest identyczna z linią II. Pomiędzy kątem // i kątem 0 istnieje zależność:

„    b

tg// = sin oraz c =-—

COS0

Podobne zależności zachodzą dla naprężeń efektywnych. Przy dużej liczbie badań jest wygodniej poprowadzić linię II (ryc. 48) niż linię wytrzymałości styczną do kol Mohra. len sposób ułatwia uśrednianie wyników badań oraz, po bardzo prostym przeliczeniu, określenie kąta tarcia wewnętrznego i spójności gruntu (w praktyce dla kątów o niskich wartościach przyjmuje się często, że rzędna początkowa ^ jest równa spójności c i // = <P).

10 I ahoratoryjr* badani* 145