pkm osinski20

38 l Konstruowanie maszyn

Na skutek ograniczeń wynikających ze szczegółowych zasad konstrukcji przedział(j ten ulega zawężenia Niektóre zmienne decyzyjne mogą przyjmować dowolne warto-; śti ż ciągłego przedziału [.v_l0tW .v_(mJ, a inne mogą przyjmować tylko wartości, dyskretne Wynika to ze względów technologicznych lub normalizacyjnych. Zmienne, decyzyjne, takie jak: moduły kół zębatych, wymiary połączeń śrubowych, kołków,, sworzni, łożysk tocznych iłp., są ściśle określone przez normy, a więc zakres ich i I zmienności zawęża się do zbioru liczb dyskretnych. Inne wartości są dyskretnej z założenia, np. liczby zębów w kołach zębatych muszą być całkowite. Zdecydowana' I większość ograniczeń ma charakter nićrównościowy, ale w pewnych sytuacjach mogą, I one być w postaci równościowej. Przykładem może być ograniczenie nn przełożenie: I przy doborze liczby zębów koła i zębnika. Ograniczenie to może być sformułowane' I w postaci równościowej lub nierównościowcj. Często postać ograniczeń jest bardzOj I złożona, a sprawdzenie, czy ograniczenie jest spełnione, czy nie. wymaga wielu. I skomplikowanych obliczeń pomocniczych, co wiąże się nieraz z wywoływaniem I złożonych podprogramów, służących do sprawdzania ograniczeń pomocniczych., I Przykładem może być sprawdzenie ograniczeń wytrzymałościowych pary walcowych: I kół zębatych za pomocą łożonego podprogramu, wykonującego wiele skomplikować I nych obliczeń wstępnych, co przedstawiono w pracach [9,19, 23].

W procesie budowy modelu matematycznego wszystkie ograniczenia wynikające ze szczegółowych zasad konstrukcji muszą być przedstawione w postaci jednoznacz-: I nej matematycznie, tak aby dla dowolnego wektora zmiennych decyzyjnych można I było jednoznacznie stwierdzić, czy należy on do zbioru rozwiązań dopuszczalnych, a więc czy są spełnione wszystkie ograniczenia, czy też nie. Zbiór punktów w przestrzeni zmiennych decyzyjnych, w których spełnione są wszystkie ograniczenia] narzucone na konstrukcję, nazywamy zbiorem dopuszczalnym lub zbiorem rozwią- I zań dopuszczalnych

(1.5)

Zbiór dopuszczalny d> ma zwykle charakter dyskrctno-ciągły, gdyż niektóre zmienne decyzyjne mogą przybierać tylko wartości dyskretne, a inne — dowolne wMtoto z zadanego przedziału. Należy pamiętać, że każda informacja zapisana | w pamięci komputera ma charakter dyskretny (wynika to z binarnego zapisu! informacji), W komputerze można co najwyżej zrealizować dyskretny podzbiór skończenie wymiarowej przestrzeni R°. Błędny byłby jednak wniosek, że badania (w lym optymalizację) trzeba ograniczyć do takich zbiorów. Dyskretność zbioru, chociaż upraszcza rozumowanie przy niewielkiej liczbie jego elementów, utrudnia jednak efektywne badanie (w tym wybór) przy bardzo dużej liczbie elementów. Jeśli różnice na poziomic kroków dyskretyzacji nie odgrywają większej Toli, to często wygodniej jest zakładać, że zbiór dopuszczalny ma charakter ciągły.

Konstrukcja spełniająca pierwszą ogólną zasadę konstrukcji (a ściślej — wektor zmiennych decyzyjnych x) musi należeć do zbioru rozwiązań dopuszczalnych d>. Matematyczny zapis tej zasady jest następujący:

(1.6)

xe $<=£,.

Konstrukcja należąca do zbioru dopuszczalnego 0 jest poprawna (dobra), a konstrukcja nie należąca do zbioru 0 jest niedobra (rys. 1.13). Liczba ograniczeń nicrównościowyeh określających zbiór dopuszczalny może być dowolnie wielka, byleby tylko zbiór ten nie był pusty, gdyż oznacza to, że przy tak ostrych ograniczeniach nic istnieje żadna konstrukcja dopuszczalna. Przy budowie zbioru dopuszczalnego należy unikać ograniczeń sformułowanych w postaci równościowej, gdyż ograniczenia te utrudniają numeryczne przeprowadzenie obliczeń optymalizacyjnych. W przypadku ograniczeń równościowych należy raczej dążyć do zmniejszenia liczby zmiennych decyzyjnych, traktując ograniczenia równościowe jako przepis na obliczanie jednej ze zmiennych decyzyjnych. Takie postępowanie zmniejsza wymiarowość zadania (już Einstein mówił o „przekleństwie” wymiarowości), znakomicie ułatwiając badanie (optymalizację), a nie zmniejszając stopnia szczegółowości modelu. Przykłady takiego postępowania przedstawiono w pracy [19].

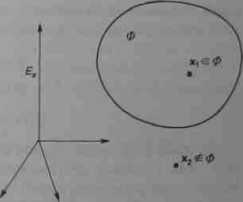
Rys. 1.13. Ilustracja pierwszej ogólnej zasady konstrukcji

W celu wyboru ze zbioru rozwiązań dobrych rozwiązania najlepszego konieczne jest ustalenie kryteriów jakości konstrukcji. Druga ogólna zasada konstrukcji mówi, żc konstrukcja powinna być optymalna (polioptymalna) w danych warunkach ze względu na przyjęte kryterium (kryteria) optymalizacji. Dobór kryteriów jest zadaniem bardzo odpowiedzialnym i złożonym. Zadanie optymalizacji można postawić w kategoriach działania praktycznego: osiągnięcie pożądanego efektu przy minimum nakładu, lub osiągnięcie maksimum efektu przy wykorzystaniu dozwolonych nakładów. Reguły tc mają charakter praw ekonomicznych i już w tym podejściu widać, jak istotny jest dobór kryteriów i do jak różnych wyników mogą prowadzić różne kryteria. Szczególnie niebezpieczne jest uleganie kryteriom wyłącznie ekonomicznym. Maksymalizacja zysku lub minimalizacja kosztów nie powinny być jedynymi kryteriami w procesie wyboru rozwiązania ze zbioru dopuszczalnego. Może tp prowadzić do niebezpiecznych skutków ekologicznych, społecznych,« nawet technicznych. W procesie konstruowania należy przede wszystkim uwzględniać kryteria techniczne, nie zapominając o ekonomicznych. Kryteria techniczne wynikają z zasad konstrukcji. Są to kryteria funkcjonalności, niezawodności trwałości, sprawności, lekkości, ekonomiczności, łatwości eksploatacji, tcchnologicznowi