Scan0034

©J. Pelc WM 1767

Z

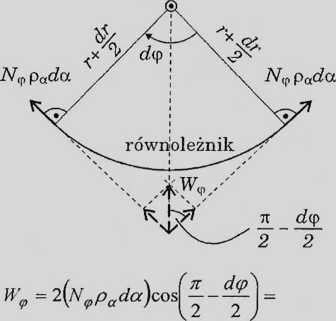
= 2{N_vp_ada)s in^ = (n _ęp_ada)dę

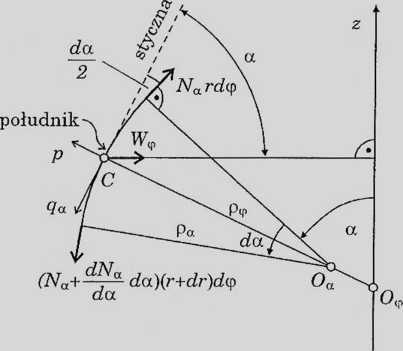
Równania równowagi sil

1) w kierunku stycznym do południka:

N_ard(p cos-~— + f A'_a +    da \r + dr)dę cos    - 2 N_ęp_ada cos a: sin •+ q_ard<pp_ada = 0

Po wymnożeniu i pominięciu małych wyższego rzędu oraz po podzieleniu przez czynnik dcpda jest:

d(r- N )

. ^g ~ N p_a cos aO + q_arp_a = 0    (1)

da

2)    w kierunku obwodowym <p jest tożsamościowo spełnione (ze względu na warunek obrotowej symetrii powłoki).

3)    w kierunku prostopadłym do elementu powłoki:

ntoj(r + dr)d<psin^ + N_ard<psin^- + {n_vp_adad(p)s\x\a - prdcpp_ada = 0 (2) Uwzględniając zależność (r = p_ę sin aj, po przekształceniach otrzymujemy

g    8

2    2

Ponieważ N_v = \<J_ędr = <j_p jdr = gcr_ę i podobnie N_a = ga_a, to równanie Laplace’a

_g    _g

2    2

można zapisać w naprężeniach:

^₊Ą^ ₌

P<p Pa

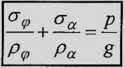
P

<- równanie Laplace’a    (3)

(3’)

Za pomocą równań (3) i (1) możemy wyznaczyć siły wewnętrzne, gdy znamy obciążenie oraz promienie krzywizn powłoki. Dodatkowo, równanie różniczkowe (1) można zastąpić algebraicznym równaniem równowagi sił działających na część powłoki odciętą płaszczyzną prostopadłą do osi obrotu z.

PRZYKŁAD 1. NACZYNIE KULISTE

Naczynie kuliste poddano działaniu ciśnienia wewnętrznego p [N/m²]. Obliczyć naprężenia błonowe w ściance naczynia.

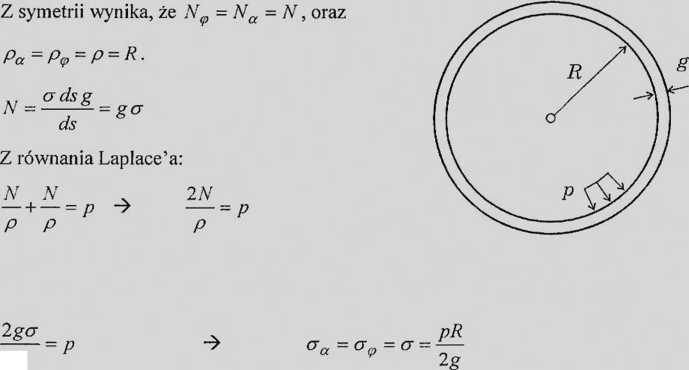
R