Scan0006 2

©J. Pelc WMT.doc/11

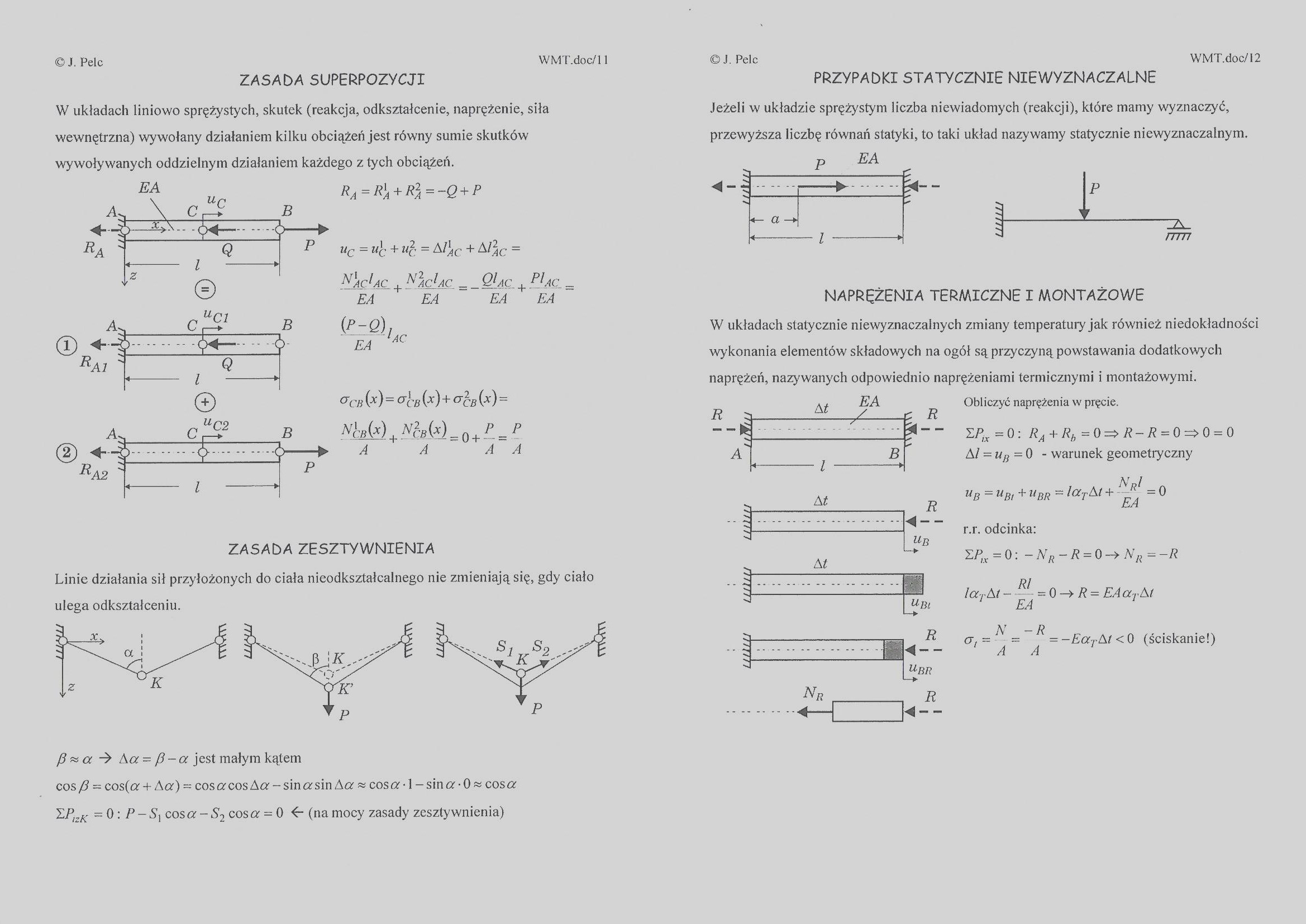
ZASADA SUPERPOZYCJI

W układach liniowo sprężystych, skutek (reakcja, odkształcenie, naprężenie, siła wewnętrzna) wywołany działaniem kilku obciążeń jest równy sumie skutków wywoływanych oddzielnym działaniem każdego z tych obciążeń.

R,

EA

Ra = R'a + R²a=-Q+p

\ C ^    B

---$>-£>N-- -(j)^ ......(S—

Q

R Uq — u\- + ifi- = Al\_c + A l_AC =

©

RAft AC ₊ NacJac _ _ QIąC ₊ PIac EA EA EA EA

R

Al

C A    B

- -<£—<>•

/4C

Q

©

/(

C_r-i B

4........<P-.......Ą-

A2

ZASADA ZESZTYWNIENIA

Linie działania sił przyłożonych do ciała nieodkształcalnego nie zmieniają się, gdy ciało ulega odkształceniu.

fi » a -> Aa = /? - a jest małym kątem

cos fi - cos(a + Aa) = cos a cos Aa-sin a sin Aa « cosa-1 - sina -0 w cos a Y.P_lzK = 0 : P-S_] cosa - S₂ cos a = 0 <r (na mocy zasady zesztywnienia)

PRZYPADKI STATYCZNIE NIEWYZNACZALNE

Jeżeli w układzie sprężystym liczba niewiadomych (reakcji), które mamy wyznaczyć, przewyższa liczbę równań statyki, to taki układ nazywamy statycznie niewyznaczalnym.

p EA

◄-t	_ . .___L.				P f
		W
	«- a —►	— 1-*	** "V. V	1
				mn

NAPRĘŻENIA TERMICZNE I MONTAŻOWE

W układach statycznie niewyznaczalnych zmiany temperatury jak również niedokładności wykonania elementów składowych na ogół są przyczyną powstawania dodatkowych naprężeń, nazywanych odpowiednio naprężeniami termicznymi i montażowymi.

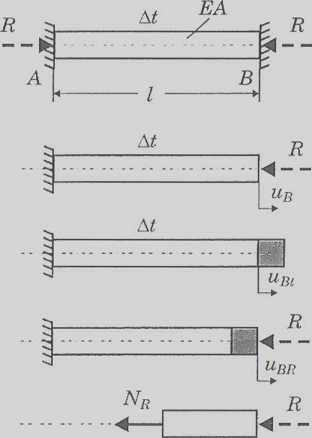
Obliczyć naprężenia w pręcie.

ZP_ix= 0: R_a + R_h = 0 => R - R = 0 => 0 = 0 Al - u_B = 0 - warunek geometryczny

¹¹B = ^uBt + ^UBR = ^la7^At +    = ⁰

r.r. odcinka:

2/T = 0: - N_P -R = 0 -> A'» - -A

la_rAt ----- = 0 -> /? = EAa_rAl EA

a, = ^    ^ = -Ea_rAt < 0 (ściskanie!)

/I zł