Scan0044

©J. Pelc    WMT/87

Po skorzystaniu z warunków brzegowych: u₂ = v₂ = w₃ = v₃ = u₄ = v₄ = 0 (formalnie po

wyzerowaniu wierszy i kolumn macierzy' K odpowiadających tym stopniom swobody i wstawieniu jedynek na główną przekątną tej macierzy) otrzymamy:

EA

3

0.884    -0.212

-0.212    1.716

10.0

5.0

detK = 1.472

Ad. 4.

Mnożąc lewostronnie to równanie przez odwrotność macierzy K otrzymujemy:

3	1.716	0.212'	I^100]	3
1A12EA	0.212	0.884	1 5.0 j	~ ea _

1.166 1.144 1.144 0.600

“l V]

Ad. 5.

Z prawa Hooke’a Al

Pl_

EA

P=^EA Al

l

₌ _3_fl2. 5.0{ EA{ 4.44

10.0

38

Wyznaczenie sił wymaga więc obliczenia wydłużeń prętów. Otrzymamy je transformując przemieszczenia (wynik rozwiązania układu równań MES) z układu globalnego (x,y) do układów lokalnych poszczególnych prętów, zgodnie z wyprowadzoną wcześniej regułą u=tu.

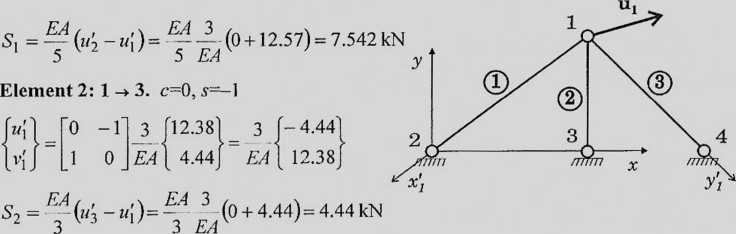
Element 1: 1 -> 2. c=-0.8, s~0.6

U\

c s -s c

c s - s c

3

EA

J 12.381 { 4.44J

- 0.8	-0.6“	3	fl2.38]	_ AJ	-12.57 1
0.6	1 oc o l	EA	k 4.44J	EA	3.876J

© J. Pelc

WMT/88

Element 3: 1 -> 4. c=0.707, j=-0.707

0.707	-0.707"	3	[12.38]	3	[ 5.6141
0.707	0.707 _	EA	[ 4.44J	~ EA	[11.89 J

S₃ = ^EA-(u'₄-ul)= ^EA— (O-5.614)= -5.614kN (ściskanie!) 5    3 £/i

PROGRAMY KOMPUTEROWE, BIBLIOTEKI ELEMENTÓW, ZAKRESY MOŻLIWYCH ANALIZ INŻYNIERSKICH.

(Internetowe bazy wiedzy)