Scan0013 (13)

© J. Pelc WMT.doc/25

I _v. = ——— h-    cos 20 - I _vv.sin 20

2 2 '

U +    ^ i 2^

^y 2 2 ^y

\x~\v

l_xy = I^cos2(9 + ——¹-sin 26

Ekstremalne wartości I_x>=Ii, ly=h nazywamy momentami głównymi figury względem osi (1,2). Jeśli ponadto osie (1,2) maja początek w środku ciężkości figury to osie te nazywamy głównymi centralnymi osiami bezwładności figury, odpowiednie zaś momenty - głównymi centralnymi momentami bezwładności figury

dl

Jeżeli funkcja 1(6) osiąga ekstremum, to = 0.

dO

d I_r.

_ 2 j

= -(l_v-i_v)sin2(9-2i_v>.cos2(9 = 0 —» tan2#₀ = ^A>

dO    I ,v I y

Kąt 0_O - ^ arctan

'-2 I_Xy'

określa kierunki głównych osi bezwładności (1,2).

Można sprawdzić, że

[i .v' (00 ) - Iekstr» I v' (Po ) I eksli^l

. _x    2\_xv v    x'=\, y'=2    <=> Ix'y'(Po) ⁼ 0

I.v’v' (#o) = 0 <=> tan 29₀ =- j    ->

I.v I v

Ekstremalne wartości momentów bezwładności (momentów głównych):

I_x+l_v

/ ,2= ' ±

1,2    ₂

+1²

ⁿ 1 xy

Przykład 2. Momenty bezwładności koła

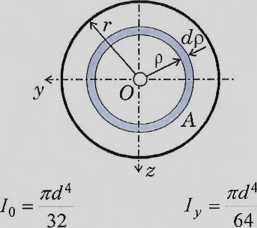
/₀ = jp²dA = Jp²{2.7tp-dp)=27t\p^2,dp = 2n:^r = ⁷¹¹

a    o    o    4    2

n fd V _ n d⁴ _ nd^A 2 v 2 J ^_ 2 16 “ 32

,    ,    r    r    r    ~ r    *    -    7td'⁴

/₀ = /,.+/,=/,.+/,,= 21 - -> 1 _v —

⁰    > ^z >    >    >    32    >    64

Przykład 3. Momenty bezwładności trójkąta. Koło Mohra-Landa

Przykład. Obliczyć momenty \_y, i_y \_{y Zc}

hy(C)

I_y = Jz²dA = J jC²dr)d£ -

A    0 0

u (y{ę) \    ^h ( (r\\    "    "

\e \dn dc = k²ko‘ k=fc²Ac)Jc=jm

o V o J    o    o    o

ft-f A

y(()=^ah(h-()=a-^ah(

I_yĄ(¹dA_yĄ^\a-^\dę=a

a

^{1>V I v} W ^A 12    9 2

3 h 4

12 18

-i/?

/?³ /7³^    ah³

Jo

3 4

36

12