ScanImage16

32 —

2. Różniczkowanie

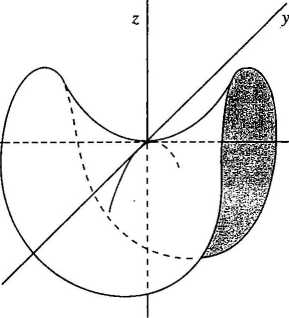
odwrotnego do twierdzenia 2.6 bywa'łatwo dostrzegalna dla n > 1. Niech na przykład funkcja /: M² -> R będzie określona wzorem f(x, y) = x² — y² (rysunek 2.2). Wówczas Di/(O, 0) = 0, ponieważ gi ma minimum w 0, podczas gdy D₂/(0, 0) = 0, ponieważ g₂ ma maksimum w 0. Oczywiście (0, 0) nie jest ani względnym maksimum, ani względnym minimum.

32 —

2. Różniczkowanie

x

Rys. 2.2

Jeżeli twierdzenie 2.6 zostanie zastosowane do znajdowania maksimów lub minimów / na A, to wartości / w punktach brzegowych muszą być rozpatrywane osobno — niemiłe zajęcie, ponieważ brzeg A może być całym zbiorem A. Zadanie 2.27 wskazuje jak to zrobić, a zadanie 5.16 podaje lepszą metodę, która może być często stosowana.

Zadania

2.17.    Znaleźć pochodne cząstkowe następujących funkcji:

(a)    f(x,y, z) =x?.

(b)    /(*, y, z) = z. j

(c)    f(x,y) = sin(x siny).

(d)    f(x, y, z) = sinj(.xsin(ysinz)).

(e)    f(x, y, z) =x^yZt.

(f) f(x,y,z)=x>+*.    „

(g)    f(x, y, z) = (x+y)^z.

(h)    f(x, y) = sin(xy).

(i) f(^x> y) — [sin(j:y)]^cos3.    *.

2.18.    Znaleźć pochodne cząstkowe następujących funkcji (gdzie g: M M jest

ciągła):

(a)    f(x, y) = f*^+y g.

(b)    f(x, y) = f* g.

Pochodne cząstkowe

(c)    f(x, y) = f*^yg.

(d)    f(x,y) = f^^g) g.

2.19. Znaleźć D₂f{ 1, y), jeżeli

f(x, y) = x^x* + (Iogx){arctg[arctg (arctg (sin(cosxy) - log(x + y)))]}-Wskazówka. Można to zrobić w prosty sposób.

2.20.    Wyrazić pochodne cząstkowe funkcji / za pomocą pochodnych funkcji g i h, jeżeli

(a)    /(x,y) = g(x)h(y).

(b)    f(x, y) = *(*)*«.

(c)    f(x, y) = g(x).

(d)    f(x, y) = g(y).

(e)    f(x,y) = g(x + y).

2.21. * Niech g\,g₂: R² -*■ R będą ciągle. Określmy /: R² -> R jako

x    y

f(x,y) = J gi(t,0)dt + J g₂(x,t)dt.

o    o

(a)    Pokazać, że D₂f(x, y) - g₂(x, y).

(b)    Jak określić /, aby zachodziło D\f(x, y) = gi(x, y)?

(c)    Znaleźć taką funkcję /: R² -» R, że D\f(x, y) — x i D₂f(x, y) = y. Następnie znaleźć taką /, że D\f(x, y)-y\ D₂f(x, y) = x.

2.22* Pokazać, że jeżeli /: R² -*■ R i D₂f = 0, to / nie zależy od drugiej zmiennej. Pokazać, że jeżeli D\f = D₂f = 0, to / jest stała.

2.23.* Niech A = {(jc, y) € R²: x < 0 lub x > 0 i y / 0}.

(a)    Pokazać, że jeżeli /: A —► R i D\f = D₂f = 0, to / jest stała.

Wskazówka. Zauważmy, że dowolną parę punktów w A można połączyć łamaną,

której każdy odcinek jest równoległy do jednej z osi.

(b)    Znaleźć taką funkcję /: A —> R, że D₂f = 0, lecz / zależy od drugiej zmiennej.

2.24. Określmy /: R² -» R jako

Jt² — y²

/(*. y)

xy' 29 ’ §^dy (*- y) ^ °>

x² + y^z

0,    gdy (x, y) = 0.

(a)    Pokazać, że D₂f(x, 0) = x dla wszystkich x i Di/(0, y) = —y dla wszystkich y.

(b)    Pokazać, że D\,2 /(0,0) ^ D₂,i/(0,0).

2.25.* Określmy /: R -

/(*) =

wzorem

₀—X^-

e^_JC“², gdy x ^ 0,

0, gdy x = 0.

Pokazać, że / jest funkcją klasy C°° oraz /^(l)(0) = 0 dla wszystkich i.