sciaga9

Twierdzenie 6.1.7 (Fermata', warunek konieczny istnienia ekstremum) Jeżeli funkcja / ma

1.    ekstremum lokalne w punkcie x₀,

2.    pochodną/'(ro),

to

/'(*o) = 0.

Twierdzenie 6.1.13 (U warunek wystarczający istnienia ekstremum) Jeżeli funkcja / spełnia warunki:

1.    /'(*o) = /"(xo) = ... = /<"-»(xo) = 0,

2.    /<">(x_o)<0,

3.    n jest liczbą parzystą, gdzie n £ 2,

Definicja 6.2.1 (funkcja wypukła)

Funkcja / jest wypukła na przedziale (a,b), gdzie -oo ^ o < 6 ^ oo, jeżeli

A A /(Axi + (l-A)r,UA/(*_ł) + (l-A)/(x_a).

«<».<«><» 0<A<1

Definicja 6.2.4 (funkcja wklęsła)

Funkcja / jest wklęsła na przedziale (a. 6). gdzie -oo $ a < b $ oo. jeżeli

A A /(A*i + (1 ~ A)xj) ^ A/(x,) + (J — A)/(xj).

«<*!<*»<» 0<A<1

Twierdzenie 6.3.2 (warunek konieczny istnienia punktu przecięcia,/ Jeżeli funkcja / spełnia warunki:

1    (x₀, / (x₀)) jest jej punktem przegięcia,

2. istnieje/"(xo), to

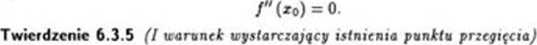
Jeżeli funkcja / spełnia warunki:

1. w punkcie xo ma pochodną właściwą lub niewłaściwą,

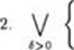
*> o l

/"(x) < 0 dla każdego x € S (*ó,t), f"(z) > 0 dla każdego x € S (x£,6),

to (xq./(xo)) jest punktem przegięcia jej wykresu.