0368

369

§ 5. Ekstrema, wartości największe i najmniejsze

Uwaga I. Warunek konieczny istnienia ekstremum można krótko napisać jeszcze tak:

df(x₁,x₂,...,x_n)=0,

bo jeśli fx_l=fx2 ⁼ ---⁼fx„—0,^to dla wszystkich dx_x, dx₂, ..., dx„ jest zawsze df(x _x,x₂,...,x_n)    dx _x +f_X2 dx₂ +... +J_Xn dx„ = 0.

Przy tym jest i na odwrót — jeżeli równość df=0 jest spełniona tożsamościowo w pewnym

punkcie, to wobec dowolności dx₁, dx₂, ..., dx„ każda z pochodnych f_Xt, f'_Xi.....f_Xn musi

być równa zeru.

Uwaga II. Zazwyczaj rozpatrywana funkcja f(x_x,x₂,...,x_n) ma skończone pochodne cząstkowe w całym obszarze i wówczas punktów, w których funkcja ma ekstremum, należy szukać tylko wśród punktów stacjonarnych. Zdarzają się jednak przypadki, gdy w oddzielnych punktach niektóre pochodne cząstkowe mają wartości nieskończone lub w ogóle nie istnieją, podczas gdy pozostałe są równe zeru. Punkty takie należy wraz z punktami stacjonarnymi zaliczyć do tych, które podejrzewamy o ekstrema (patrz niżej ustęp 201, 6)).

197. Warunki dostateczne (przypadek funkcji dwu zmiennych). Podobnie jak w przypadku funkcji jednej zmiennej, w punkcie stacjonarnym wcale nie musi być ekstremum. Na przykład dla prostej funkcji z=xy, pochodne z'_x=y, z'_y=x są jednocześnie równe zeru jedynie w punkcie (0,0), w którym z=0. Jednocześnie widać bezpośrednio, że w dowolnym otoczeniu tego punktu funkcja przybiera zarówno wartości dodatnie jak i ujemne, a więc nie ma w nim ekstremum. Na rysunku 92 (str. 301) przedstawiona jest powierzchnia (paraboloida hiperboliczna) określona równaniem z=xy. W pobliżu początku układu ma ona kształt podobny do siodła, pewne jej pionowe przekroje są wypukłe w dół, inne w górę.

Powstaje tym samym zagadnienie, jakie są warunki dostateczne dla istnienia (lub nieistnienia) ekstremum w punkcie stacjonarnym, a więc jakim dodatkowym badaniom należy poddać te punkty.

Rozpatrzymy najpierw przypadek funkcji dwóch zmiennych/(x, y). Załóżmy, że funkcja ta jest określona, ciągła i ma ciągłe pochodne cząstkowe pierwszego i drugiego rzędu w otoczeniu pewnego stacjonarnego punktu (x₀, y₀). W punkcie tym jest zatem

(la)

/*'(*o,yo)=o>    fy(x₀,yo)=°-

Dla ustalenia, czy rzeczywiście funkcja ta ma w punkcie (x₀, y₀) ekstremum czy nie, naturalne jest rozpatrzyć różnicę

A=f(x,y)-f(x₀,y₀).

Rozwińmy ją według wzoru Taylora [195] ograniczając się do dwóch wyrazów. Ponieważ punkt (x₀, y₀) jest z założenia stacjonarny, pierwszy wyraz znika i otrzymujemy po prostu

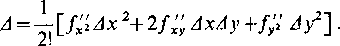
(2)

24 G. M. Fichtenholz