0380

381

§ 5. Ekstrema, wartości największe i najmniejsze

z dodatkowym warunkiem, że suma ich jest stała

(.p-x)+(p-y)+(p-z)=3p-2p=p.

Wiemy już (ustęp 200, przykład 3)), że iloczyn jest największy, gdy wszystkie czynniki są równe, a więc gdy x=y=z=jp. Otrzymujemy znów trójkąt równoboczny.

3) Spośród wpisanych w elipsoidę

prostopadłościanów o krawędziach równoległych do jej osi znaleźć ten, który ma największą objętość.

Jeśli przez x, y, z oznaczymy współrzędne tego z wierzchołków, który leży w pierwszym kącie trójściennym układu, to objętość P=8jcyz. Zamiast V można rozpatrywać wielkość

V² x² y² z² “~64 a²b²c²⁼S'lS'V’

ponieważ obie wielkości osiągają oczywiście wartość największą dla tych samych x, y, z. Dla u zaś zagadnienie sprowadza się znów do przykładu 3) z poprzedniego ustępu.

Odpowiedź:

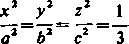
tak że x——y=—=,

V 3    V³

z

c

V³'

4) Przypuśćmy, że jakiś gaz, na przykład powietrze, zostaje sprężony w kompresorze tłokowym od ciśnienia atmosferycznego p₀ do ciśnienia p> p₀. Praca zużyta przy tym na sprężenie 1 gramoczą-steczki gazu wyraża się wzorem

A=RT₀

y-1

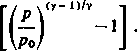
R jest stalą gazową, T₀ — temperaturą absolutną gazu przed sprężeniem, a y pewną liczbą większą od 1, zależną od konstrukcji kompresora. Praca A jest oczywiście tym mniejsza, im mniejsza jest temperatura początkowa T₀ . Przy dużych sprężeniach, gdy oszczędność zużytej pracy jest ważna, rozbija się cały proces sprężania na pewną liczbę stopni, między którymi ochładza się gaz nagrzewający się przy sprężaniu.

Przypuśćmy, że mamy do czynienia z kompresorem trójstopniowym, z dwoma pośrednimi chłodzeniami obniżającymi temperaturę znów do T₀. Jeżeli oznaczymy przez pi i p₂ ciśnienie po pierwszym i drugim stopniu sprężania, to cała praca sprężania będzie teraz równa

<y- 1)/»

A=RT₀

y—i

......-■]}

Powstaje zagadnienie jak przy danych p₀, p i T₀ wybrać ciśnienie Pi i p₂, aby zużyta, praca była najmniejsza.

Jeżeli się odrzuci stały czynnik i stały składnik, które nie wpływają na szukane wielkości pi i p₂, to zagadnienie sprowadza się do badania wyrażenia

, (V- D/y

(y-i >/v

Ponieważ iloczyn

-er"-®......’♦£)

er*®.......GT-®

(y- l)/ł

zachowuje stalą wartość, więc korzystając z przykładu 4) z ustępu 200 wiemy od razu, że suma osiąga