0384

385

§ 5. Ekstrema, wartości największe i najmniejsze

to prawdziwe w przypadku n dodawanych sinusów (zatem największą wartością ich sumy jest nsin — ). Pokażemy, że wówczas jest tak również dla rozpatrywanej sumy n+1 sinusów.    ”

Zgodnie z ogólna wskazówką zrobioną wyżej, trzeba porównać wartość (n+1) sin- z wartoś

ciami, które funkcja przybiera na brzegu obszaru 2.

Weźmy w tym celu np. ścianę x„=0 sympleksu. Na niej u jest funkcją tylko n—1 zmiennych:

M=sinx₁+sinx₂ + ...+sinx„_₁+sin [2jc— (xi+jc2 + ...+jc„_i)J

i zgodnie z założeniem największą jej wartością jest nsin —. To samo można stwierdzić i dla pozosta-

n

łych ścian. Ale ponieważ

2ir    2ji

nsin — <(n + l)sin- (²),

n    n + 1

twierdzenie jest udowodnione. Największe pole ma zatem wielokąt foremny.

8) Rozpatrzmy sieć elektryczną zasilającą z połączeniem równoległym. Na rysunku 110 przedstawiony jest schemat sieci, przy czym + i B są zaciskami źródła prądu, a P,, P₂...../^J„ odbiornikami

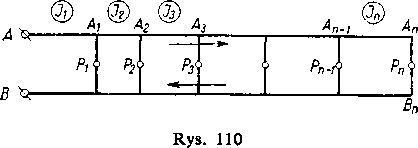
prądu pobierającymi odpowiednio prądy    Dany jest z góry dopuszczalny ogólny spadek

napięcia w sieci równy 2e. Trzeba określić takie przekroje przewodów, aby na całą sieć główną poszła możliwie mała ilość miedzi.

Oczywiście wystarczy ograniczyć się do rozpatrywania jednego z przewodów, powiedzmy AA„, bo drugi przewód znajduje się w dokładnie takich samych warunkach. Oznaczmy przez l\,l₂, l„ długości części AA_ip A_tA₂,A,-iA_n w metrach, i przez q_L, q₂,..., q_n — pola ich przekrojów poprzecznych w mm². Wówczas wyrażenie

U=‘hqx + /2?2 + ... + /n?n

przedstawia objętość całej zużytej miedzi w cm³. Musimy znaleźć najmniejszą wartość tego wyrażenia pamiętając przy tym, że ogólny spadek napięcia w przewodzie AA„ powinien się równać e.

Łatwo obliczyć, jakie prądy J_lt J₂.....J„ będą przepływać w odcinkach AA i, A_tA₂.....A„-xA„

sieci, mianowicie

Jx-h + i₂ + ... + i„,    j₂ — l2 + i3 + ..+<n,    Jn — in-

Jeżeli oznaczymy przez p opór przewodnika miedzianego o długości 1 m i przekroju 1 mm², to opory tych odcinków sieci będą równe

Ph    ph    Ph

r i=—,    r₂ = —,    ...,    r„=--

q i    q ₂    qn

(^l) Fakt ten wynika z tego, że funkcja--maleje monofonicznie, gdy z rośnie od 0 do Jt (patrz

ustęp 133, 1)).    ^Z 25 G. M. Fichtenholz