skanowanie0008 2

> dzielimy obie strony przez D"¹ i otrzymujemy: x=D"¹(b-(L+U)x), po wy mnożeniu dostajemy ostateczny wzór iteracyjny:

x⁽ⁱ⁺¹)=-D'¹(L+U)x⁽ⁱ⁾+D"¹b

0

1

*22

0

o

0	1- O	”1 _1
0	0
1 *33	0	h
0	1 *44	IaJ

"(/+!)"		i "u	0	0	o^-	f	'0	0	0	0'		"0	U\ 2	W, 3	^U\A	\
Y(W) A2		0	1 *22	0	0		*2,	0	0	0	+	0	0	U 23	^U24		X?	+
v(/+l)	^1' .																#
		0	0	1 °33	0		hl	In	0	0		0	0	0	«34
v(/+l) .4		0	0	0	1 *44 _	V		h 2		0		0	0	0	0	/	x<‘> L^A4 J

i=l..n

Z tego wzoru obliczamy kolejne przybliżenia x.

W programie będziemy liczyć w pętli kolejne współrzędne przybliżenia rozwiązania ze wzoru:

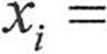
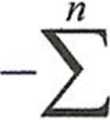
j=i j*i

x°.a_ija_jj +

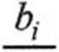
C.

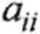
(po wykonaniu działań na macierzach i wektorach po prawej stronie)

> Jako pierwsze przybliżenie rozwiązania przyjmujemy dowolny wektor x₀. Niech dla i=l..n Xj=l/i:

1

1

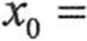
2

1

3

i

4

> Kryterium zakończenia obliczeń:

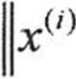
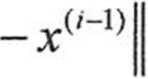
< Eps

liczba kroków k.

Eps>0, dowolnie małe oraz po wykonaniu nie więcej niż ustalona