skanowanie0008

> dzielimy obie strony przez D"¹ i otrzymujemy: x=D'¹(b-(L+U)x), po wymnożeniu dostajemy ostateczny wzór iteracyjny: x^<i+1)—D"^I(L+U)x^<i)+D"'b

		~ i	0	0	0'	/	0	0	0	0		0	ul2	^U13	«14	>			i	0	0	0'	V
Y(t+i) ^x2		0	1 ^a22	0	0		h,	0	0	0	+	0	0	^U23	«24		ę	+	0	1 °22	0	0	b2
V(M) ■*3		0	0	1 "13	0		hi	hi	0	0		0	0	0	“34		4^n		0	0	1	0	b.,
v(ł+l) .4		0	0	0	£	k	}n	hl	hi	0		0	0	0	0	y	m		0	0	0	1	A.

i=l..n

Z tego wzoru obliczamy kolejne przybliżenia x.

W programie będziemy liczyć w pętli kolejne współrzędne przybliżenia rozwiązania ze wzoru:

n    %

ZO , b,

^xj^au^aij

m

j*i

(po wykonaniu działań na macierzach i wektorach po prawej stronie)

>• Jako pierwsze przybliżenie rozwiązania przyjmujemy dowolny wektor xo. Niech dla i=l..n Xj=l/i:

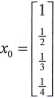
> Kryterium zakończenia obliczeń:

[L«> II < v_vs

II    W ^y , Eps>0, dowolnie małe oraz po wykonaniu nie więcej niż ustalona

liczba kroków k.