skanuj0013 2

dzieląc stronami, otrzymamy:
z b - = -tgy u a
ponieważ
Z
U
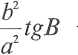
czyli'
b
tgym-tgB
a
* = 7
a
tgy = Vl - e2tgB
OR
z
sinij/
z = bsiny
OP^b
Kąt y można zdefiniować przez rzutowanie punktu P wzdłuż promienia równoleżnika na sferę o promieniu b. Rzut punktu P na sferę ma współrzędne geograficzne ą/, L.
Wyszukiwarka
Podobne podstrony:
szablon sprawozdania z prawem archimedesa02 Ponieważ: pw = p0-p*gVPc=P0~PcgV stąd PcgV = P0-Pc PwgY
4 (2471) oraz dzieląc (1.3) i (1.4) stronami otrzymujemy wzór na impedancję Z badanego dwójnika (1.5
Strona0067 67 Po odjęciu od siebie tych równań stronami otrzymano:(2.160) Ponieważ przy małym tłumie
skanuj0044 (7) Dodajemy stronami równania: 10 i podwojone 2°; otrzymujemy: 3° Cr2072" + H20 + 2
skanuj0044 Dodajemy stronami równania: 10 i podwojone 2°; otrzymujemy: 3° Cr2072 + H20 + 2 CH>CO
Strona0056 56 2[Act)0 - ^]cos t = O, czyli A-—^— (2.118) 2®0 Otrzymano więc ostate
41199 skanuj0044 (7) Dodajemy stronami równania: 10 i podwojone 2°; otrzymujemy: 3° Cr2072" + H
skanuj0056 (Kopiowanie) krzywą C = f (t) otrzymujemy1: CO 00 (8.8)AUC -
P1120619 [1024x768] 213 213 Dzieląc powyższe równania stronami, otrzymujemy
Strona0056 56 2[Act)0 - ^]cos t = O, czyli A-—^— (2.118) 2®0 Otrzymano więc ostate
2.4a. Temperatura a energiakinetyczna, c. O dzieląc stronami równania (2) i (3) otrzymujemy ni=r}2 O
DSC05205 a po podzieleniu obu równań stronami otrzymujemy: (2.61)n, _ Aba Ponieważ obydwie ciecze wy
CCF20091008�053 Analogicznie zapisując: i dzieląc licznik i mianownik ułamka przez V, otrzymuje się:
skanuj0070 140 140 (4.7) (4.8)dę=_jw_ dr ^+^,1+^,2 Przyrównując stronami (4.6) i (4.7) otrzymujemy r
41199 skanuj0044 (7) Dodajemy stronami równania: 10 i podwojone 2°; otrzymujemy: 3° Cr2072" + H
skanuj0017 (24) stąd otrzymamy N} = G] cos 60°, r, =/iiVj =/iGjCos60o. (D-18.10) G
więcej podobnych podstron