skanuj0046 4

124 Przepływ energii

K_m =

k²(u₂ - u, )(z₂ - z,)

(In—)²

z,

(7.20.)

Jak to zostało omówione w rozdziale 4. pionowe gradienty prędkości wiatru, ciśnienia pary wodnej i temperatury są odwrotnie proporcjonalne nie do wysokości nad powierzchnię czynną z, ale do z - d, gdzie d jest wysokością przesunięcia płaszczyzny zerowej.

Korzystając z powyższego stwierdzenia, z równania 7,20. oraz z teorii podobieństwa, że w stanie równowagi obojętnej K_M=K_H-K_V, możemy sformułować ostateczne równania na strumienie pędu, pary wodnej i ciepła wymieniane pomiędzy-' dwoma poziomami w atmosferze w warunkach stacjonarności przepływu i w stanie równowagi obojętnej, które pozwalają na wyliczenie wartości gęstości tych strumieni na podstawie pomiarów prędkości wiatru, ciśnienia pary wodnej i temperatury tylko na tych poziomach:

k(u₂ - u,)

(7.21.)

ln(-

E_t=-

p_a e k'(u₂ - u!)(c₂ -ej)

Z -ł o

p(ln—r

z.

(7.22.)

Pą ■ £j> • k²(u₂ - U|)(T₂ -T.)

,    o

(In -^r Z]

(7.23.)

Strumień pary wodnej przepływający od powierzchni czynnej do atmosfery' transportuje jednocześnie strumień energii. Ten strumień energii równa się iloczynowi strumienia pary wodnej E, i utajonego ciepła parowania L. Równanie 7.15. można napisać w formie:

LE

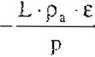
^Kv dz

(7.24.)

wprowadzając współczynnik y (stała psychrometryczna) określony wzorem:

Y = ■

VP

Le

(7.25.)

otrzymujemy po przekształceniu:

*

Porównując równanie 7.21. z równaniem 4.8. widać, że wyrażenie w nawiasach jest równe prędkości tarciowej u„.