Wektory płaszczyzna

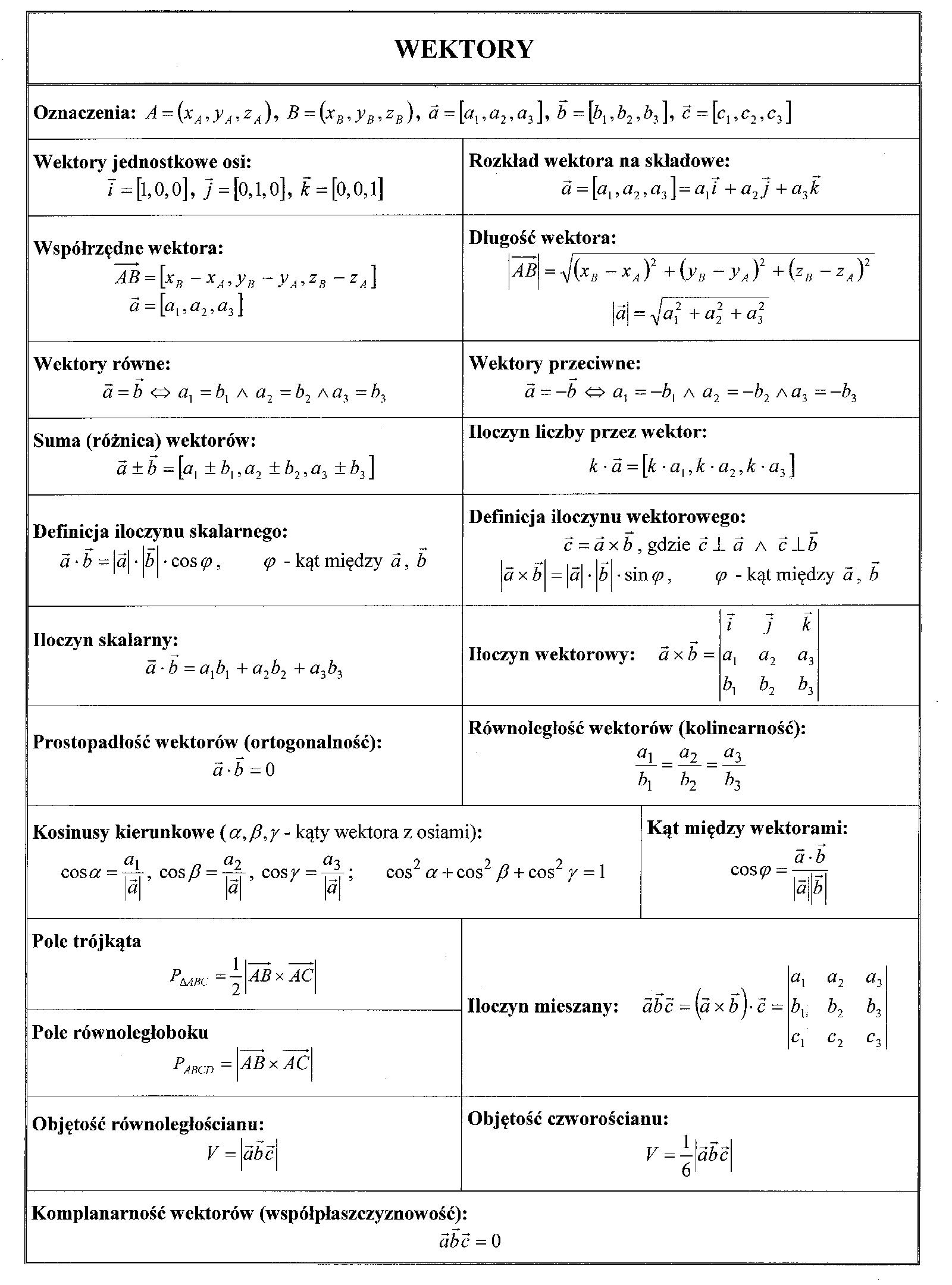
WEKTORY

Oznaczenia:    A = (x_A,y_A,z_A), B = (x_B,y_B,z_B), a = [a„a₂,a₃], b =[6₁,*₂,*₃]₎ c =[c,,c₂,c₃]

Wektory jednostkowe osi:

i = [1,0,0], 7 = [0,1,0], k = [0,0,1]

Rozkład wektora na składowe:

a = [a_l,a₂,a₃\ = a_li + a₂j + a₃k

f G^ + Cl2 H" cfi

Współrzędne wektora:

AB = [x_b-x_A,y„

Cl ⁼ [tl2| 5 Cl2 , Cl^ J

Długość wektora:

^A£\ = ^(^XB ~^XaY +(^8 - ya)² +(^Z» ~^zaY

\a\ = Ja

Wektory przeciwne:

Wektory równe:

a = h ca a_] = b_x a a₂ = b₂ a a₃ = b₃

d — -b <=> a_] - -b_{ a a₂ = —b₂ a a₃ = —b₃

Suma (różnica) wektorów:

a ± b = [^| ± &|, a₂ ± 6₂, a₃ ± b₃ ]

Iloczyn liczby przez wektor:

k • a = [k • a,, k • a₂, & • a₃ ]

Definicja iloczynu skalarnego:

5 * £ = |3| • 6 • cos p, ę - kąt między 5, £

Definicja iloczynu wektorowego:

c ~axb, gdzie c JL a a c_Lb

* sin <p, ę - kąt między a, 6

Iloczyn skalarny:

d‘b -a_xb_x + a₂&₂ + a₃b₃

\dxb

lal

			_
	i	7	k
Iloczyn wektorowy: axb =		a2	a3
		b2	b3

Prostopadłość wektorów (ortogonalność):

= 0

Równoległość wektorów (kolinearność):

b\    ^3

Kosinusy kierunkowe (a, fi,/- kąty wektora z osiami):

^a\    o ^a2    ^a3

cosa = ■—*, cosfi = —■, cosy =

7    7    7

cos a + cos fi + cos y = 1

Kąt między wektorami:

d'b

cos ę =

a

\a\

a

\a\b

Pole trójkąta

MUC

ABxAC

Iloczyn mieszany: abc ~{axb\c

Pole równoległoboku

a i	a2	^al
h	b2	b.,
	c2	^3

ARCD

ABxAC

Objętość czworościanu:

56 c		F = —	abc
		6

Objętość równoległościanu:

V =

Komplanarność wektorów (współpłaszczyznowość):

abc = 0