24396

(iv) la = a.

Długość wektora

Jeśli wektor a ma współrzędne [x_a, y_a. z_a\ to jego długość jest wyrażona wzorem:

Własności długości wektorów są podobne jak własności długości wektorów' na płaszczyźnie:

(i)    |a + 6| < |a| + |6|,

(ii)    |aa| = |a||a|.

Wektor a nazywa się wersoreni jc*śli |a| = 1. Wersory, który są położone na osiach nazywamy wersoraini osi i oznaczamy je i dla osi Oj, j dla osi Qy, k dla osi Os. Jak łatwo zauważy' wersory osi mają współrzędne: i = [1,0,0]. j = [0,1,0],Ar = [0.0,1], Jeśli a.b.c są trzema wektorami, a a,/?,7 skalarami to aa + /?6 + 7c nazywamy liniową kombinacją wektorów a, b, c.

Każdy wektor da się jednoznacznie przedstawić jako liniową kombinację wer-sorów i,j,k. Jeśli wektor a ma współrzędne x_a, y_a. z_a to

a = x_ai + ijaj + z_ak.

Rzeczywiście a = [x_a, y_a, z_a) = x₀[l. 0,0] + y_a[0,1,0] + 2_a[0.0.1] = x_ai + y_aj +

Z_ak.

Wektory a. 6, c nazywamy komplanarnymi wtedy i tylko wtedy gdy istnieje płaszczyzna do której te wektory są równoległe. Inaczej mówiąc wektory a. b, c są komplaname wtedy i tylko wtedy gdy jeden z nich jest liniową kombinacją pozostałych wektorów, np. a = 3b + 7c.

Iloczyn skalarny

Iloczynem skalarnym wektorów a = [x\,y\,Z\] i 6 = [z^,!/2> nazywamy liczbę rzeczywistą X\X₂ + 1/12/2 + Z\Z₂ i oznaczamy ją przez a o b.

Własności iloczynu skalarnego

Niech a,b,c będą trzema wektorami, i niech o będzie skalarem, wtedy iloczyn skalarny ma następujące własności:

(i)    (a + 6) o c = a o c + b o c,

(ii)    (aa) 06 = a(a o 6) = a o (ab),

(iii)    ao6 = 6 o a,

(iv)    aoa>0iaoa = 0 +=> a = 0.

Ponadto można zauważyć, że |a| = \Ja o a.

Kątem między wektorami a i b nazywamy mniejszy z kipów, wyznaczonych przez przecinające się proste w yznaczone przez te wektory. Kąt między wektorami a i b wyznaczony jest wzorem:

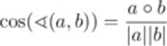
2