00098501

290

Inwersja. Funkcja realizuje odwzorowanie zwane inwersją, przy czym obrazem punktu z — 0 i⁸* *1 w = co i na odwrót. Odwzorowanie to jest jednokrotne na całej płaszczyźnie . Gaussa. Funkcja (111.94) jest holomorficzna na całej płaszczyźnie z wyjątkiem p ktu z = 0. Inwersja odwzorowuje konforemnie całą płaszczyznę Gaussa na nil sarną, gdyż zachowuje ponadto kąt skierowany między każdymi dwoma kierunkami wyprowadzonymi z punktu 0 albo ».

Funkcję-(EH.94) można traktować jako złożenie następujących odwzorowań;,

1*    — TT5-*

Pierwsze z tych odwzorowań, to przekształcenie przez promienie odwrotne, nato* j miast drugie jest symetrią wzglfdem osi rzeczywistej.

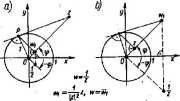
Na rys. 1U.23 jest przedstawiona. konstrukcja, na podstawie której znąjąC^, punkt z (różny od 0 i od co) można znaleźć jego obraz w ^wzorowaniu (ni.94)jp Rysunek IIL23a dotyczy przypadku, gdy [zj > 1. Jeżeli |z| =* 1, to odwzorowanie^ przez promienie odwrotne jest po prostu przekształceniem tożsamościowym, wifto inwersja (HS.94) ogranicza się do symetrii względem osi rzeczywistej. JetoU'| 0 < |z| < 1, to obraz punktu z w inwersji (01.94) znajdujemy z konstrukcji .praetk/J stawionej na rys. IIL23b.    f \

Odwzorowanie (III.94) przekształca wzajemnie jednoznacznie obszar |sj < Afet ,(tzw. kolo jednostkowe) na obszar |wj > I, do którego należy punkt w nieskoń* czoności.    '■

Inwersja ma dokładnie dwa punkty niezmiennicze, które znajdujemy z warunku . !

1 . ■ . . , . ' z =—, mianowtciez! = — 1 iz,= 1. _k

Homografia- Omawiana ostatnio inwersja należy do -ważnej w zastosowaniach klasy odwzorowań homograficznych. Są to odwzorowania postaci

_w = SE±*    cnws)

cz+d

przy czym a, b, e i d oznaczają liczby zespolone spełniające warunek

*-E

Jeżeli a = d=Ói b = c=\, to homografia (UI.95) jest inwersją (III.94), jeżeli natomiast c = 0, to homografia tą jest funkcją pierwszego stopnia.

Omówimy niektóre właściwości przekształcenia 011.95). Obrazem punktu

z — —w tym przekształceniu jest punkt w nieskończoności Jeżeli c 5* 0 (tzw. homografia właściwa), to dzieląc az+b przez cz+d można równość 0IL95) zapisać następująco

-A 1

" cz+d ^T c

Z równości tej wynika, odwzorowań:

: homografia właściwa jest superpozycją następujących ł° w, = cz+d    v

»>2 = -

fi

(m.96)

3‘    «,+ i

a więc jest superpozycją funkcji pierwszego stopnia, inwersji i ponownie funkcji pierwszego stopnia. Ponieważ każde z tych odwzorowań przekształca konforemnie płaszczyznę Gaussa na płaszczyznę Gaussa, więc tę samą właściwość ma odwzorowanie homograficzne.

Dla preykładu rozpatrzymy odwzorowanie obszaru

0< Rez< +oo, —co <lmr<0

za pomocą tomografii

vń& pierwsze z odwzorowań (01.96) jest tożsamościowe, drugie jest inwendą, trzecie jest postaci w “ —»»+!. Na rys. III.24 przedstawiono rozwiązanie tego przykładu.