0084

85

§ 1. Pojęcie funkcji

geometrycznym rozważanej funkcji i nazywa się jej wykresem. Przy tych umowach samo równanie y=f (x) nazywa się równaniem krzywej AB.

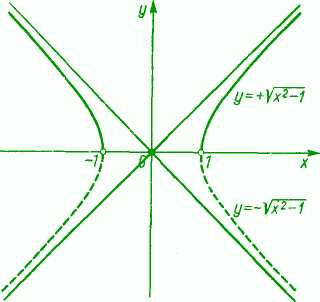
Na przykład na rysunkach 6 i 7 przedstawiono wykresy funkcji

y=±V l-x²    (|x|<l) oraz y=±Vx²-l (|x|>l),

w których czytelnik rozpozna okrąg i hiperbolę równoboczną. Czytelnik w najbliższych ustępach znajdzie wiele dalszych przykładów graficznego przedstawienia funkcji. Zazwyczaj buduje się wykres z punktów.

y y= M
-2 -1 0	*12 3
	-1
	-2
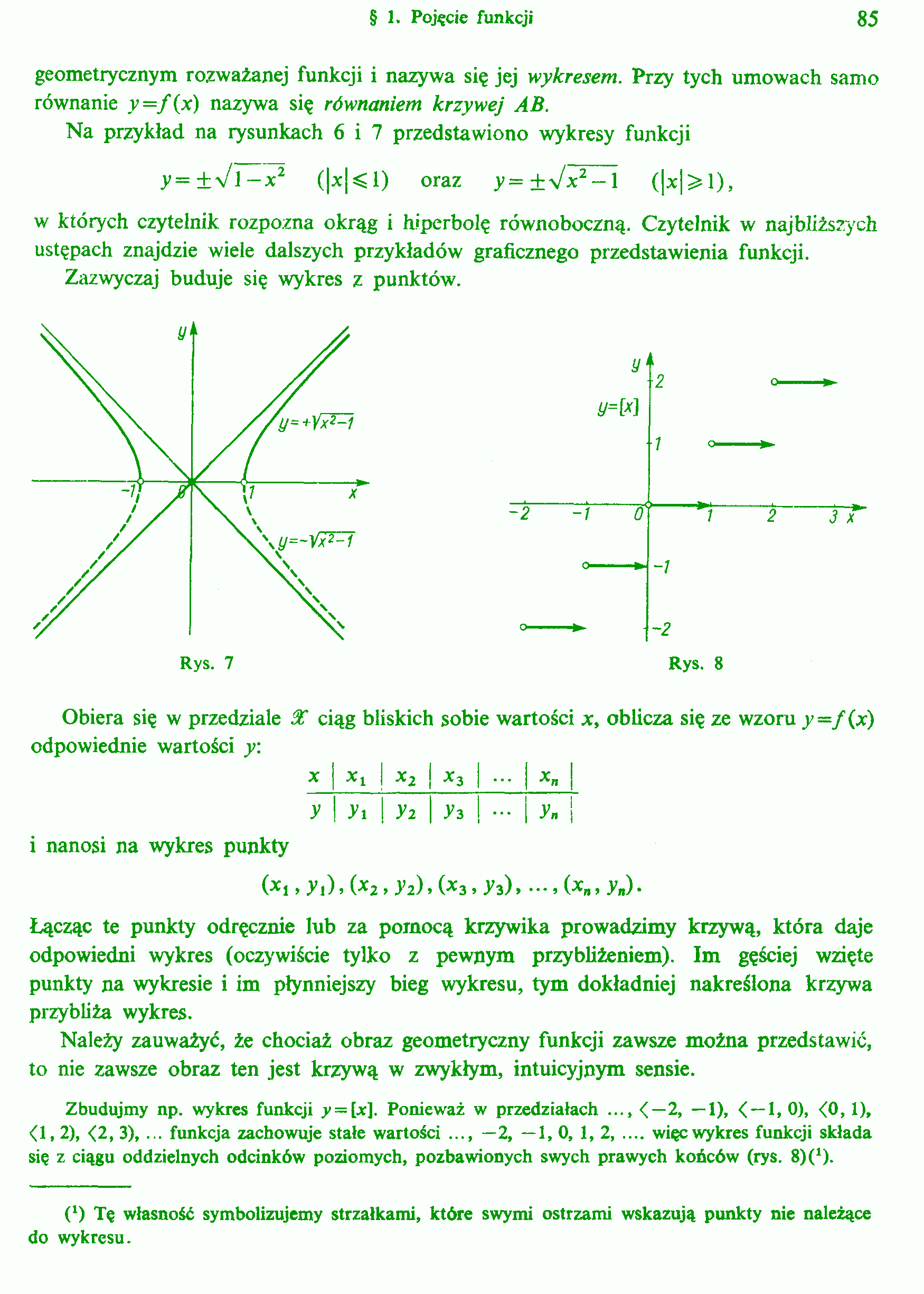
	Rys. 8

Obiera się w przedziale X ciąg bliskich sobie wartości x, oblicza się ze wzoru y=f(x) odpowiednie wartości y:

X | Xi |	*2 | *3 |	3
y | Ti	yi | Ts	I ... i i

Rys. 7

i nanosi na wykres punkty

(*i, >b) > (*2, yi). (*3»y*), —, (*», y_n) •

Łącząc te punkty odręcznie lub za pomocą krzywika prowadzimy krzywą, która daje odpowiedni wykres (oczywiście tylko z pewnym przybliżeniem). Im gęściej wzięte punkty na wykresie i im płynniejszy bieg wykresu, tym dokładniej nakreślona krzywa przybliża wykres.

Należy zauważyć, że chociaż obraz geometryczny funkcji zawsze można przedstawić, to nie zawsze obraz ten jest krzywą w zwykłym, intuicyjnym sensie.

Zbudujmy np. wykres funkcji y = [x]. Ponieważ w przedziałach ..., <—2, —1), < —1, 0), <0,1),

<1,2), <2, 3), ... funkcja zachowuje stałe wartości ..., —2, —1, 0, 1, 2.....więc wykres funkcji składa

się z ciągu oddzielnych odcinków poziomych, pozbawionych swych prawych końców (rys. 8H¹).

(‘) Tę własność symbolizujemy strzałkami, które swymi ostrzami wskazują punkty nie należące do wykresu.