011

71-/2    I- 71-/2

sin t = u cos t dt = i = O ti — 0 t — 7t/2 =>• 7X = 1

4tt£ł² ■ 3 j sin³ ty sin²1 cos²1(cos²1 4 sin²1) dt — lina² f sin⁴1 cos t dt o    ^v    o

12?ra² J u^A du — o

E. MOMENT STATYCZNY I BEZWŁADNOŚCI, ŚRODEK CIĘŻKOŚCI

Niech dany będzie trapez krzywoliniowy ograniczony prostymi y = 0, x = a, x = f> oraz krzywy = /(t), gdzie /(#) >0 dla a < x < b. Załóżmy, że jest on wykonany z materiału jednorodnego o gęstości p. Oto wzory na moment statyczny względem osi Ox (oznaczony przez M_x) i osi Oy (oznaczony przez M_y), oraz na moment bezwładności względem osi Ox (oznaczony przez B._T) i osi Oy (oznaczony przez B_y)\

Mc = ip/ [/(a:)]^2 a		^MV = P fa ^dx^
b		b
^BX = yj [/(a:).	dx,	By = pj x^2f(x) dx.
a		u

Środek ciężkości podanego trapezu krzywoliniowego to punkt

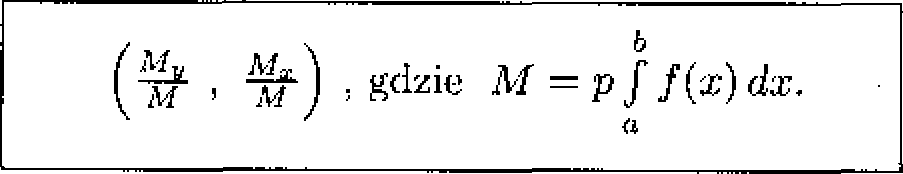
PRZYKŁAD 11. Obliczyć momenty statyczny oraz bezwładności (względem obu osi) trójkąta o wierzchołkach (0,0), (1,0), (0,2). Znaleźć środek ciężkości tego trójkąta.

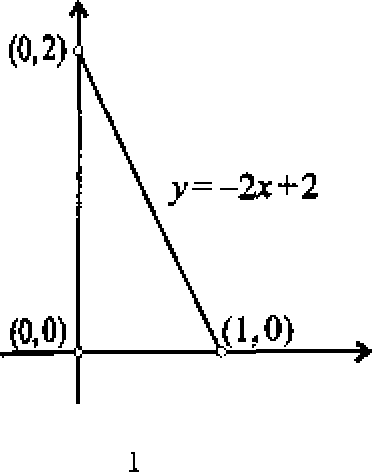
Trójkąt podany jest na rysunku obok. Widzimy, że prosta y = —2x 4- 2 jest równaniem przed wproś tokątnej. Czyli f(x) = —2x-\-2. Jeżeli nie zostało podane p, to przyjmujemy, że p = 1,

i

Stosując wzory z ramek otrzymamy: M_x — ^ j (—2x4 2)² dx =

o

-Ł    1

/(2x? - 4x 4- 2)dx = |x³ - 2x² -\- 2x — | - 2 4 2 = |,

□    o

i    i    i

M_y = / x(-2x 4 2)    = /(—2x² 4- 2x)    = -|x³ 4^²    = ^,

O    0    '0

B_x = |/(-2x 4- 2)³dx = | /(—4- 3x² - 3x 4 l)dx = -|x⁴ + |z³ - 4x² 4-o    o

B_y — f x²(—2x 4 2) dx = /(~2x³ 4 2x²)    = ~^x⁴ 4 §x³

o    o

^{1 1}

o

Ponieważ M = J(— 2x 4 2)dx = —x² 4 2x = 1, więc środkiem ciężkości trójkąta jest punkt (^,    §)>