DSC07132 (6)

192

Całki nieoznaczone

< = U*

dt m . dl. coo * m

/(2*mx + 3cosx) dx _ f cosi___dx_

2008*1 J sin?* _{| ;} cos*:

t *z

d) / -TT-

y sin icc

/:

= h,(t6’x + 2) ₊ ^arctg(^)_+C7. dt

₌ [

J i

- /^^A = ^ln(^t?+²) + ²#-ctg^f

fi-«»

“/«*(i*«^ł) /

—d£

**(*“ 0(‘ + l)

1

i. + _2_ + —Ł £² £ + 1 £ - 1

= -i + iMł + I|-|lń|£-l| + C

=— + -łn £ 2

t-ll⁺ sini ⁺ 2*^D|«inz- 1-1

+ C.

t) Funkcja wymierna R zmiennych u = sini, v = coaz, tworząca funkcję podcałkową, raa postać

^R^^u’^{v) =} TZ~2-

l + V?

Ponieważ funkcja ta spełnia warunek R(u,-v) = -R(u, v), więc w całce dokonamy podstawienia t = sini. Wówczas otrzymamy

-J-TT-T*

* = ilm di a COlzdl

/cos*xdz f(l-ain^Jx) ct»xdx 1+sia** J    l + śin²z

- 2Ń££} = —-3£ + 4arctg£ + C

■ -3ńnx + 4arctg(ainx) + C.

0 Przełuztalearay funkcję podcałkową do postaci

sin z

tgz + 4 sinx + 4cosz'

Funkcja wymierna R zmiennych u = sin x, u = cos z, tworząca funkcję podcałkową,

wyraża się wzorem IUu,v) = —-—, Ponieważ funkcja ta spełnia warunek Rl—u, -u) =

u + 4o    *

Przykłady

R(u,v), więc podstawiamy t = tg*. Wtedy mamy

f sin x dx J sin x + 4 cos

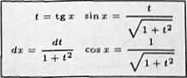
.    L__.

= / _Vl + i? ' 1 + O

vT+t*⁺7f+ż?

t + 4

«^a + l

* t* +1

| r ^tdt_₌ [

J (t + 4)(l+f) J

__4 f dt 4_ T tdt i r

17 J t + 4 ⁺ 17 J t* + l ⁺ tf I

= ~ln|t + 4| + -ln (t^a + l) + i_{arclgl +} ę

= In |tg* + 4| + ^ In (tg² x +1) + ±arctg(tgx) +C

4    . V .*. •    1

= — — In |sinx + 4cosx| + —x + C.

Całkowanie funkcji z niewymiemościami

• Przykład 7.7

Obliczyć podane całki z funkcji niewymiernych:

_cyjlZzldz-,    d) J y/x* + 25dx.

Rozwiązanie

a) Podstawiamy x = 3sin t, gdzie — ^ $ t ^ Wtedy ^9-1* = 3cost oraz dz = 3costdt. Dalej mamy

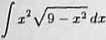
J 9 sin² t ■ 3 cos t • 3 cos tdt =

j J sin² 2t dt

b) Podstawiamy x Osiej mamy

= — [t -cost(sint-2sin^at)] +C = 1 aresin f - 5n/^ (| - |f)]    ^

2sli C, gdzie t S R. Wtedy v/*^a + 4 = 2cht oraz dz =

• /' -•