018

18

L Zdarzenia i prawdopodobieństwo

1.1.9.    W urnie jest nty3 białych i n)^3 czarnych kul. Obliczyć prawdopodobieństwo wylosowania trzech czarnych kul, gdy kule losujemy

a)    bez zwracania,

b)    ze zwracaniem.

1.1.10.    Niech (O, ó?, Pr) będzie przestrzenią probabilistyczną, gdzie Q — [0,1] oraz Pr jest prawdopodobieństwem geometrycznym. Niech A = [0,a], B = [b, 1], gdzie 0 ^ a < b ^ 1. Czy da się tak dobrać parametry a i b, aby zdarzenia A i B były niezależne?

1.1.11.    Ze zbioru liczb {2,3,5,30} wybieramy losowo jedną. Określmy zdarzenia:

A - wylosowano liczbę parzystą,

B - wylosowano liczbę podzielną przez 3,

C - wylosowano liczbę podzielną przez 5.

Czy zdarzenia te są niezależne? Czy niezależne są dwa dowolne zdarzenia?

1.2. Prawa

wielkich liczb i symulacje

1.2.1. Mocne i słabe prawo wielkich liczb

Według potocznych opinii, jeżeli przeprowadzając n obserwacji zaobserwujemy interesujące nas zjawisko k razy, to prawdopodobieństwo zajścia tego zjawiska powinno wynosić k/n. Iloraz ten jest często przyjmowany za tzw. „statystyczną definicję prawdopodobieństwa”. Określenie to nie jest całkiem poprawne, ale intuicyjnie uzasadnione, a poniższe twierdzenia nadają mu ścisły matematycznie charakter.

Mocne prawo wielkich liczb

Twierdzenie 1.2.1.

Niech (0,^,Pr) będzie przestrzenią probabilistyczną, a {A_i £    bę

dzie nieskończonym ciągiem zdarzeń niezależnych o tym samym prawdopodobieństwie Pr(A₍) — p. Niech 0) £ O będzie dowolnym, ale ustalonym zdarzeniem elementarnym. Oznaczmy przez N(n,co) liczbę tych zdarzeń A_i spośród A _{,..., A_n, dla których (O £ A-, gdy i= 1,2,..., n. Wtedy

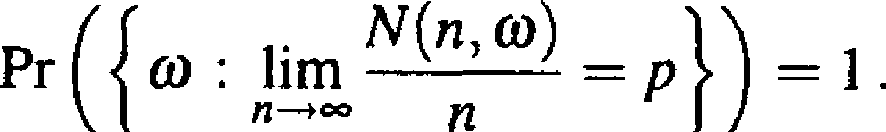
Twierdzenie 1.2.2.

Przy założeniach z twierdzenia 1.2.1 dla każdego £ > 0 zachodzi równość

(1.2.1)

Słabe prawo wielkich liczb

lim Pr

N(n, co)

--p

n

> £

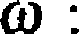
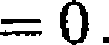
(1.2.2)