0204

205

§ 4. Pochodne i różniczki wyższych rzędów

Słuszność jego dla «= 1 oraz n = 2 można sprawdzić bezpośrednio. Przypuśćmy teraz, że wzór ten jest słuszny dla wszystkich wartości n do pewnego «>2 włącznie; udowodnimy, że pozostanie on wtedy słuszny przy zmianie n na n + 1 ('). W tym celu rozpatrzymy wyrażenie

D" ^{+ 1}(x"e^1/1)=iyiD(x’e^llx)]=Dⁿlnxⁿ-^le^l,x-x’-²e^ll1]=nD"(x’-¹e^ll1)-DlD"-¹(x"-²e^u1)].

Korzystając z naszego założenia możemy to napisać w postaci

„l/¹ r    1/¹^

cbdo. Wzór ten jest więc słuszny dla wszystkich wartości naturalnych n.

117. Wzór Leibniza. Jak zauważyliśmy na początku poprzedniego ustępu, reguły I i II z ustępu 97 można przenieść i na pochodne dowolnego rzędu. Sprawa komplikuje się w przypadku reguły III dotyczącej różniczkowania iloczynu.

Załóżmy, że funkcje u, v zmiennej niezależnej x mają każda z osobna pochodne do rzędu n włącznie. Udowodnimy, że wtedy ich iloczyn y=uv ma również pochodną rzędu n i znajdziemy ją.

Stosując regułę III, będziemy różniczkowali kolejno ten iloczyn; otrzymamy y'=u'v + uv',    y" — u"v+2u'v’ + uv",

/" = u’"v+3 u"v + 3uV' + uv"’,    ...

Możemy łatwo zauważyć prawo, według którego zbudowane są wszystkie te wzory. Ich prawe strony przypominają rozkład potęg dwumianu u+v, (u+v)², (u+v)³, ... tylko zamiast potęg u, v, występują pochodne odpowiednich rzędów. Podobieństwo stanie się jeszcze pełniejsze, jeśli w otrzymanych wzorach zamiast u, v, napiszemy m⁽⁰⁾, r^(0>. Rozszerzając to prawo na przypadek dowolnego n dojdziemy do ogólnego wzoru (²)

(1)    /=(„»)"= f    u⁽ⁿ~'V⁰ = u^ln)v + nu⁽ⁿ~¹V +    ^y("~^2)v" + • ■ • +

n(n —l)...(n —i + 1) ...    .

1    ... • i

Dla dowodu jego słuszności skorzystamy znowu z metody indukcji matematycznej.

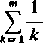
=1

1 1

_+T+T+".+

1

»

m

itd.

1

Zwracamy uwagę czytelnika na tę specyficzną formę zastosowania metody indukcji matematycznej; w rzeczywistości (patrz tekst poniżej) wykorzystujemy słuszność naszego wzoru dla n i dla n — 1, a nie tylko dla n.

(²) Symbol £ oznacza sumę składników jednakowego typu. Gdy składniki te zależą od jednego wskaźnika, zmieniającego się w określonych granicach, to granice te zapisujemy na dole i na górze. Na przykład

n

^O| = flo+Cl+ •■•+««,

1 = 0