02

14.3.3. Budowa macierzy cosinusów kierunkowych

W macierzy tej zapisane sącosinusy kierunkowe poszczególnych prętów kratownicy, a co za tym idzie, poszczególnych sil wewnętrznych. Zbudowanie tej macierzy wymaga określenia składowych długości prętów w przyjętym układzie współrzędnych oraz wyznaczenie ich całkowitej długości. Na tej podstawie możemy dopiero określić cosinusy nachylenia poszczególnych prętów kratownicy do osi układu współrzędnych.

Macierz składowych długości prętów': D = [d,\;	/ = 1,2.....n; j = 1,2.	(14.5)
obliczymy z równania (patrz (14.14))	D = - K^rX.	(14.6)
Długości prętów’ są równe (patrz (/4.15))	*'03 II	(14.7)
a ich cosinusy kierunkowe dn C.J ^= coso. — —;	/ = 1.....n;	(14.8)
	j = U.

Macierz cosinusów’ kierunkowych C ma następującą postać:

C = [c„]    (14.9)

Wiersze macierzy’ odpowiadają poszczególnym prętom kratownicy, natomiast kolumny cosinusom kątów nachylenia prętów do osi / i 2 układu współrzędnych (patrz (14.16)).

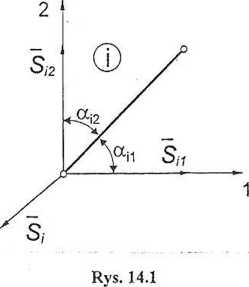
Pomiędzy siłami zachodzi następująca zależność (rys. 14.1.)

S,j = -c_vS,.    (14.10)

Zakładamy, że w węzłach kratownicy przyłożone są siły zewnętrzne, których składowe są elementami macierz)' P (patrz (14.16))

Między macierzami sił zewnętrznych P i wewnętrznych S zachodzi związek (14.2) wynikający z równowagi węzłów

P = -AS

14.3.5. Budow-a macierzy współczynników równań równowagi węzłów

Macierz A (patrz (14.17)) powstaje z macierz)' K przez podstawienie w miejsce elementów:

,.]”    - odpowiednich wierszy macierzy cosinusów kierunkowych z macierz)' C,

odpowiadających poszczególnym prętom kratownicy,

,.-1”    - jw'., ale ze znakiem przeciwnym,    v

„0”    - dwuelementowego wektora zerowego.

Wyznaczenie sil wewnętrznych wymaga wyeliminowania z macierzy A wierszy, a z macierzy kolumnowej P elementów odpowiadających w'arunkom podparcia. Po rozwiązaniu takiego uproszczonego układu równań (14.18) wyznaczymy sił)' wewnętrzne w prętach kratownicy.

Wartość dodatnia siły oznacza, że pręt jest rozciągany, a ujemna, że ściskany.

Znając wartości tych sił i korzystając z odrzuconych równań zawierających składowe reakcji możemy wyznaczyć reakcje w podporach (14.19).

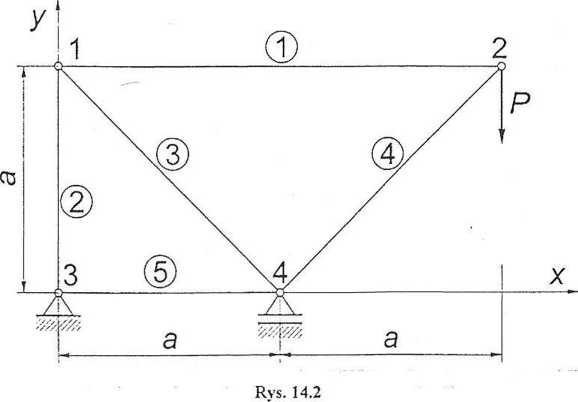
14.3.6. Przykład obliczeniowy

Dla kratownicy przedstawionej na rysunku 14.2 wyznaczyć siły wewnętrzne w prętach. Dane:    a = 2[m],

P= 10 [kNj.

- 127 -