230 (14)

Macierzą tej formy jest

B, = PA(A^rPA}"'^! A⁷ P

W podobny sposób przeprowadzimy także formę kwadratową estymatora V do formy kwadratowej wektora e. Skorzystamy tutaj ze znanego nam już związku V = ~Me. Zatem

V⁷ CT¹, V - o⁷ M⁷ C~^!. Me = e⁷BoC

z macierzą

15n - M⁷ C"¹. M

x""

Sprawdźmy jeszcze, czy wynikające z przeprowadzonych przekształceń macierze B,, B-, spełniają warunek wzajemnej niezależności następujących form kwadratowych:

H^r A^TCAi] = £⁷ B,e ~xl_._r v⁷c;!,v=r.^rB₂e -

to znaczy, czy BjC „;,B₂ =0. Istotnie

B,C_x(),B₂ ^YA(A^rl>Ay'A^TPC_x„_h M⁷C^M =

^cfu^p“¹

= o> jjPA(A⁷ PA)"¹ A^rM⁷C"j_/iM = 0 o

Pamiętając, że estymatorem współczynnika wariancji Oq jest

ml ~ —-—V⁷ PV n~ r

oraz dokonując przekształceń (/j - r,/> -n ■■■■ r)

J, ₌ 7i^1,7 A'^C«"'^{, A} 11 _ n^r A^J ffo²P.-v n ₌ i|⁷ A^rPAn ₌

- n'^rA^rPA n

r ml

możemy ostatecznie zapisać

(5.1.37)

F

n^rA^rPAn

........i.......    /]"•>'. far-n-r

^r'" 0

4) Skoro zmienna F, przyjmująca tylko wartości dodatnie (chodzi tutaj o stosunek form kwadratowych), ma ustalony rozkład, to prawdopodobieństwo, że zmienna ta przyjmie wartości mniejsze lub równe pewnej wartości można zapisać jako

W7,_/2ś/ć,) = ,

lub, uwzględniając postać zmiennej F,

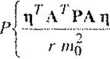
i

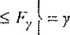
j

(5.1.38)

(przypomnijmy: y- poziom ufności). Prawdopodobieństwo (5.1.38) można także przedstawić w postaci

p{n^V A⁷ PA t] < rmlF._f }=* y    (5.1.39)

Równanie

n^r a⁷'pa n = (X - xf a⁷’pa <x - X) =    f_y

jest równaniem /-wymiarowej hiperelipsoidy o środku leżącym w punkcie o współrzędnych X. Półosie a_;, i - 1, 2,..., r tej hiperelipsoidy można wyrazić wzorem

<ij — uiqF_v    (5.1.40)

gdzie a, są wartościami własnymi macierzy A⁷PA, tzn. pierwiastkami równania (zob. np. Wiśniewski 2000)

|A⁷>A~;.I_rUo    (5.1.41)

Wartości F mogą być odczytane z tablic rozkładu F-Snedecora (tab. IV). Tablice te są tak konstruowane, że dla każdej kombinacji stopni swobody j\ ~ >'■> fi ~ » ” r i prawdopodobieństwa y są podawane takie wartości F,. że

=?

231