0395

396

VI. Wyznaczniki funkcyjne i ich zastosowania

W najprostszym przypadku — gdy równanie (1) jest algebraiczne, tj. gdy funkcja F(x, y) jest wielomianem stopnia całkowitego względem x i względem y, określona przezeń funkcja uwikłana y zmiennej x, na ogół wieloznaczna, nazywa się funkcją algebraiczną. Jeżeli stopień równania względem y nie przekracza czterech, to funkcja algebraiczna może być przedstawiona w postaci nieuwikłanej za pomocą pierwiastków, jeżeli stopień jest wyższy niż cztery, to przedstawienie takie jest możliwe tylko wyjątkowo.

Teraz będzie nas interesowało zagadnienie istnienia i jednoznaczności funkcji uwikłanej — jak również i zagadnienia dotyczące innych jej własności — niezależnie od możliwości przedstawienia jej analitycznym wzorem wyrażającym bezpośrednio y przez x. Tak postawione zagadnienie nie jest zresztą dla nas nowe, z jego szczególnym przypadkiem mieliśmy do czynienia wtedy, gdy była mowa o istnieniu i o własnościach funkcji odwrotnej i równanie    ... .    .

y-f O)=0

określało zmienną x jako funkcję uwikłaną zmiennej y.

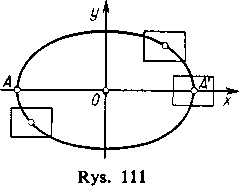
Pouczające jest geometryczne ujęcie tego zagadnienia. Przy pewnycn założeniach równanie (1) określa krzywą na płaszczyźnie (np. równanie (la) określa jak wiadomo elipsę (rys. 111)); nazywa się je w tym przypadku równaniem uwikłanym krzywej. Zagadnienie

polega na tym, czy krzywa (1) (lub jej część) może być przedstawiona zwykłym równaniem postaci y-f(x) z jednoznaczną funkcją po prawej stronie, co geometrycznie oznacza, że prosta równoległa do osi y przecina krzywą (lub jej część) tylko w jednym punkcie.

Jeżeli funkcja ma być jednoznaczna, to jak widać z przykładu elipsy, trzeba ograniczyć przy tym nie tylko obszar zmienności zmiennej x, ale i obszar zmienności zmiennej y.

Będziemy mówili krótko, że w prostokącie (a, b;c,d) równanie (1) określa y jako jednoznaczną funkcję x, jeżeli dla każdej wartości x z przedziału (a, b) równanie (1) ma jeden i tylko jeden pierwiastek y w przedziale (c, d).

Zazwyczaj będzie nas interesował określony punkt (x₀, y_Q) spełniający równanie (1) (leżący na krzywej) i rolę powyższego prostokąta spełniać będzie otoczenie tego punktu. Na przykład w przypadku elipsy (rys. 111) można oczywiście stwierdzić, że równanie (la) określa rzędną y jako jednoznaczną funkcję odciętej x w dostatecznie małym otoczeniu dowolnego punktu elipsy, z wyjątkiem jej wierzchołków A i A' leżących na dużej osi.

206. Istnienie funkcji uwikłanej. Teraz ustalimy warunki zapewniające istnienie jednoznacznej i ciągłej funkcji uwikłanej.

Twierdzenie I. Załóżmy, że

1) funkcja F(x, y) jest określona i ciągła w pewnym prostokącie 3>=(x₀-A ,x₀+A ;y₀-A', y₀+A') mającym środek w punkcie (x₀, y₀);