0445

446

VI. Wyznaczniki funkcyjne i ich zastosowania

8) Łatwo jest uogólnić przekształcenie Legendre'a na przypadek przestrzeni o dowolnej liczbie wymiarów. Niech z będzie funkcją zmiennych x%, x₂, .... x„. Przekształcenie określamy wzorami

3z

dx,

v

y x_t—-2

1 = 1    «,

(/=! , 2, ..., n);

tutaj v jest nową funkcją nowych zmiennych t_k, t₂, Założymy tutaj także, że wyznacznik

3 ^2z	3 ^2 z	d^2z
3x?	3xt dx2	3xk 3x„
d^2z	b^2 z	d^2z
3x2 3xt	3x^2	3x2 Bx„
3 ^2z	b^2z	o^2 Z
3x„ dxi	3xn 3x2	3x^2

jest różny od zera.

Zróżniczkujmy względem x_k wzór określający v traktując przy tym v jako funkcję złożoną zmiennych *1, x₂, ..., x„ za pośrednictwem z_Ł, t₂, ..., ł„:

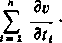
3²z _ ” ^ a²z 3x,3x_k ,=i ‘ 8x,Sx_k

(k = 1,2, ... , n).

Ponieważ J^O, wynika stąd, że

—~=x, (i=l, 2, ..., n). dt,

Wobec tego

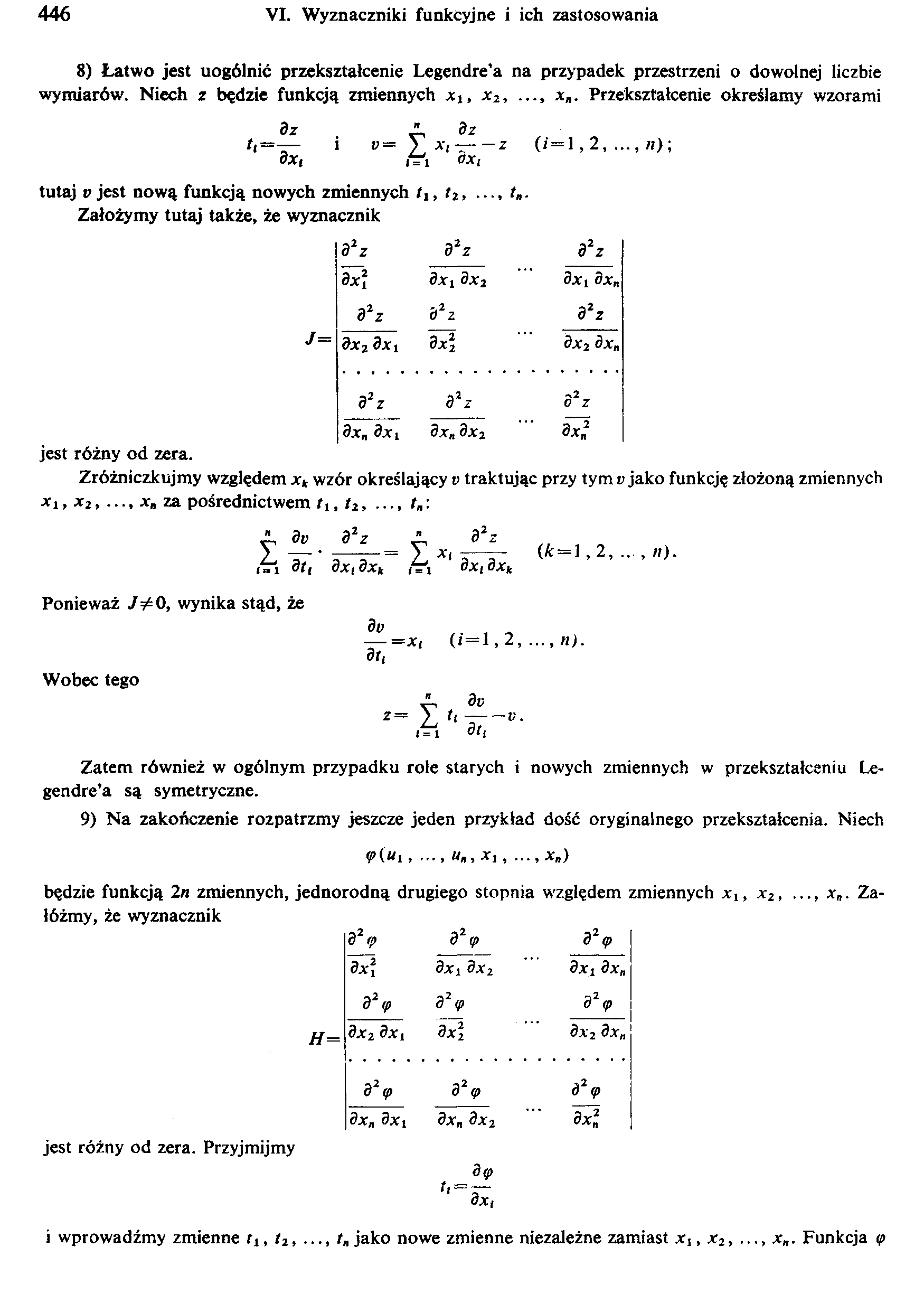
y do

:= Y t,--v.

k1    dt,

Zatem również w ogólnym przypadku role starych i nowych zmiennych w przekształceniu Le-gendre’a są symetryczne.

9) Na zakończenie rozpatrzmy jeszcze jeden przykład dość oryginalnego przekształcenia. Niech

p(#i, ... ■ x,, ..., x„)

będzie funkcją 2n zmiennych, jednorodną drugiego stopnia względem zmiennych x₁, x₂, ..., x„. Za-łóżmy, że wyznacznik

CU ■'S	B^2 ę	B^2 ę
3x1 d^2 (p	3xi Bx2 B^2 <p	3xi 3x„ B^2 q>
dx2 3xi	3x1	Bx2 3x„
B^2 (/>	B^2 tp	*2 o <p
3x„ 3xt	3x„ 3x2	3x^2n

jest różny od zera. Przyjmijmy

3ę

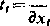
x„. Funkcja ę>

i wprowadźmy zmienne t_k, t₂, t_n jako nowe zmienne niezależne zamiast x,, x₂