0437

438

VI. Wyznaczniki funkcyjne i ich zastosowania

Dalsze pochodne najprościej jest obliczyć w następujący sposób. Wyrażenie otrzymane dla

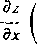
3 z \    dv    du

lub — I różniczkujemy znowu względem x (lub y) traktując pochodne — i — jako funkcje dy J    dt    du

zmiennych x i y za pośrednictwem I i u, itd.

W przypadku ogólnym, gdy wzory na przekształcenie mają postać

(21)    <P(x,y,z, ,u,v)=0,    V(x, y, z,t,u, v)=0,    0(x, y, z, I, u, o)=0

można się posługiwać dowolną z tych metod, stosując przy tym reguły różniczkowania funkcji uwikłanych.

Dla rozwiązania tego najogólniej postawionego zadania zamiany zmiennych zastosujemy teraz metodę obliczania różniczek zupełnych. Ograniczymy się do objaśnienia metody odwrotnej, to znaczy do przypadku, gdy zmienne x i y traktujemy jako niezależne i względem nich obliczamy wszystkie różniczki

Wychodząc ze wzorów (21), można przez kolejne różniczkowanie znaleźć wyrażenia

(22)    dt = a_ldx + a₂dy + a₃dz,    du=b_ldx + b₂dy + b₃dz,    dv=c₂ dx+c₂ dy+c₃ dz.

d²t —di dx² + d₂ dxdy + d₃ dy² + d_t dxdz + d_s dydz + d₆ dz² + a₃ d²z,

(23)    d²u=eidx²+...+e₆dz² + b₃d²z, d²v —fi dx²+...+f₆ dz² + c₃ d²z.

Wstawiając do równania

dv    dv

dv=— dt-1--du

dl    3 u

zamiast dt, du i dv prawe strony wzorów (22) otrzymujemy

3v    3v

Ci dx + c₂dy + c₃ dz—-— (a! dx + a₂ dy + a₃ dz) + — (6i dx + b₂ dy + b₃ dz), dt    du

stąd

(24)    dz=Adx+Bdy,

dv 3v

gdzie A i B są funkcjami wymiernymi pochodnych — i —- . Porównując ten wynik ze wzorem

dt du

dz    dz

dz = — dxĄ--dy

dx    dy

widzimy, że

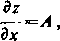
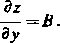
Weźmy teraz równość

d² v    , d²v    d² v    , 3v    , 3v    ₂

■z-i-dt +2——dtdu+—rdu + —d t+ — d u dt²    dtdu    du²    dt du

(t i u nie są tutaj zmiennymi niezależnymi) i podstawmy w niej zamiast różniczek dt, du, d²t, d²u, d²v znalezione dla nich wyrażenia (22) i (23), a następnie zamiast dz — wyrażenie (24). Z otrzymanej równości wyznaczamy d²z:

d²z = C dx² + 2D dxdy + Edy²;

dv    du d²v d² v d²v

współczynniki C, D i E wyrażają się wymiernie przez pochodne — , — »—-j. —— . —-=. Porów-

dt du    dt    dtdu du