0396

397

S 2. Funkcje uwikłane

2) w punkcie tym funkcja F(x, y) jest równa zeru: F{x₀, y_o)=0;

3)    przy stałym x funkcja F(x, y) monofonicznie rośnie (lub monofonicznie maleje) wraz z y.

Wówczas

a)    w pewnym otoczeniu punktu (x₀, y₀) równanie (1) określa y jako jednoznaczną funkcją y=f(x) zmiennej x;

b)    dla x=x₀ funkcja ta przybiera wartość

Fa;/(*o)=J’o;

c)    funkcja f (*) jest ciągła.

Dowód. Będziemy się najpierw przesuwali

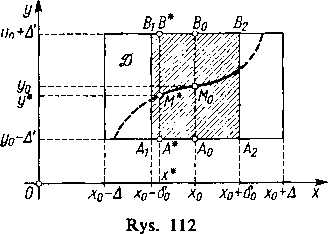
wzdłuż prostej pionowej przechodzącej przez punkt M₀(xo, y₀) (rys. 112), tzn. ustalimy x= x₀; wówczas rozpatrywana funkcja F(x, y) stanie się funkcją F(x₀, y) jednej zmiennej y.

Z założenia 2) wynika, że funkcja ta jest równa zeru dla y=y₀, a jednocześnie z założenia 3) wynika, że F(x₀, y) rośnie wraz z y. Zatem dla y<y₀ wartości jej są mniejsze od zera, a dla y>y_n — większe od zera. Wynika stąd w szczególności, że jej wartości w punktach -i4₀(x₀> yo-Aj i B₀(x₀, y₀+Aj mają różne znaki, a mianowicie

F 04_o)=F (x₀, y₀ - A') < 0 ,    F (B₀)=F(x₀, y₀ 4-.A’) >0.

Zajmijmy się teraz prostymi poziomymi przechodzącymi przez punkty A₀ i B₀, tzn. ustalmy teraz y=y₀—A' oraz y=y₀+A'. Otrzymujemy dwie funkcje F{x, y₀—A') i F{x, y₀+Aj jednej zmiennej x, które dla x=x₀ mają, jak widzieliśmy, wartości — pierwsza ujemną, druga dodatnią. Z założenia 1) wynika, że funkcje te są ciągłe (^x), a więc istnieje takie otoczenie (x₀—S₀, x₀+S₀) punktu *₀ (0<<S_o^A), w którym obie funkcje zachowują swój znak [80, lemat], tak że dla x₀ — ń₀<;c<;c₀+ń₀ jest

F(x, y₀-^')<0 , F(x, y_o+^')>0 •

Innymi słowy dana funkcja F(x, y) przyjmuje wartości ujemne w punktach odcinka A_lA₂ leżącego na dolnej podstawie wyjściowego prostokąta i wartości dodatnie w punktach odcinka B_XB₂ na górnej podstawie tego prostokąta; obydwa odcinki mają długość 2S₀ i środki odpowiednio w punktach A₀ i B₀.

Wybierzmy w przedziale (x₀—<5₀» *o+<5o) dowolną wartość x=x* i rozpatrzmy odcinek pionowy łączący punkty A*(x*, y₀—A') i B*(x*, y₀+A'). Wzdłuż tego odcinka dana funkcja znów staje się funkcją F(x*, y) jednej zmiennej y. Ponieważ jest ona na mocy 1) ciągła (²) i — jak wykazaliśmy — ma na końcach przedziału (y₀—A', y₀+A'} wartości różnych znaków

F(A*)=F(x*,y₀-A')<0,    F(B*)=F(x*, y₀+A')>0,

(‘) Założyliśmy ciągłość funkcji F(x,y) względem dwu zmiennych x i y, w takim razie jest ona ciągła względem każdej zmiennej z osobna.

(²) Patrz poprzednia notka.