skanuj0005

Równowaga trwała występuje w punkcie x₀gdyż nachylenie krzywej jest zerowe, wobec czego siła jest równa zeru, bo F(x<>)=-[    =0. Punkt materialny będący w tym x,

pozostanie trwale w spoczynku, nawer jeśli go poruszymy.to powróci do xo.

Dla x = x_iF(x₂)=0, ale gdy poruszymy punkt to F(x)=-f®g^)będzie dążyła do zepchnięcia go od tego punktu położenia. Punkt x₂nazywamy punktem równowagi nietrwałej.

W przedziale, w którym Ep jest stała, np. w otoczeniu x^ , nachylenie krzywej jest zerowe czyli też F(x )=-[ ^£-9) =0. Taki przedział nazywamy przedziałem równowagi neutralnej, ponieważ punkt materialny może być przemieszczony w otoczeniu punktu x* , a mimo to nie dozna siły przyciągającej ani odpychającej.

15 Co to jest stan metastabilny.    .

Jest to pewnego rodzaju odmiana stanu stabilnego, czyli też F(x/i... x*)=- ( ^ I =0 ale w punktach x*, x£,x^funkcja Ep(x) nie ma minimum czyli nie zachodzi:    Q

< ¹    0 X

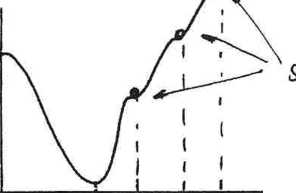
fajtasta&lni (mo-    Ódit aie

yio, SoOjf. Vy»iaJC6 jok w

X.

-V-" *i<

16    Pod jakimi warunkami energia ciała lub układu ciał jest zachowana.

Chodzi o tzw układ zachowawczy, inaczej odosobniony, nie poddany oddziaływaniom z zewnątrz. Energia ciała lub układu byłaby zachowana czyli Ec= Ek + Ep = const gdyby układ lub ciało były idealnie izolowane, tzn, żadna postać energii nie dostałaby się do ciała\układu z zewnątrz, ani żadna by nie wypłynęła. Jest to do do tej pory niemożliwe i wszystkie obecne układy są rozpraszające; np. na skutek sił tarcia zmniejsza się zasób Ek lub Ep i w związku z tym Ec układu maleje bo część została oddana na zewnątrz.

17    Co to są siły zachowawcze.

Siłą zachowawczą nazywamy siłę, jeżeli praca wykonana przez nią nad punktem materialnym poaiszającym się po dowolnej drodze zamkniętej jest równa 0. Np. siła grawitacji ( gdyby nie było sił oporów tarcia ) byłaby siłą zachowawczą, gdyż piłka rzucona pionowo do góry na pewną wysokość, wróciłaby i oddała tę samą energię kinetyczną jak nadaną przy wyrzuceniu.

18 Czy baron Munhausen mógł (jak opowiadał), ciągnąc sam siebie za włosy, wyciągnąć z błota siebie i wóz z końmi? Odpowiedź uzasadnij na zasadzie zachowania pędu.

Baron nie mógł sam siebie i wozu z końmi wyciągnąć z błota. Na podstawie zasady zachowania pędu, widać że całkowity pęd układu, a więc baron + wóz + konie, może być zmieniony tylko przez siły zewnętrzne działające na ten układ. Siły wewnętrzne ( ciągnięcie . siebie za włosy ) równe co do wartości i przeciwnie skierowane ( siłą ciągnięcia za włosy i siła oporu włosów przed wyrwaniem ), wytwarzają równe co do wartości i przeciwnie