Monotoniczność funkcji (2)

2
Wyrażenie x(2 - x) określa parabolę, która jest równa zeru w punktach x = 0, x -2. Wykres paraboli x(2 - x) pokazany jest na rysunku
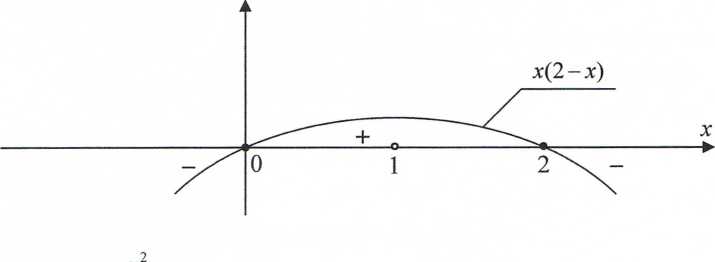
x
Stąd funkcja y(x) =-jest:
1 — x
- rosnąca w przedziałach (0,1) oraz (1, 2)
- malejąca w przedziałach (-co, 0) oraz (2, + oo)
x2
Punkt x = 1 nie należy do obszaru określoności funkcji y(x) =-.
1 -x
Zadanie 2. Zbadać monotoniczność funkcji y(x) = x + —.
x
Rozwiązanie. Funkcja y jest określona na całej osi liczbowej R z wyjątkiem x = 0 i jest różniczko walna w swoim obszarze określoności. Pochodna y jest równa
(x-l)(x + l)
,( , , 1 x2-l
y (x) = 1--T = ——
X X
Znak wyrażenia ——+ ^ zależy od znaku licznika, gdyż mianownik jest większy od zera x
w każdym punkcie osi liczbowej R z wyjątkiem punktu x = 0, w którym jest równy zeru. Wyrażenie (x - l)(x +1) określa parabolę, która jest równa zeru w punktach x = -1 , x = 1. Wykres paraboli (x - l)(x +1) pokazany jest na rysunku
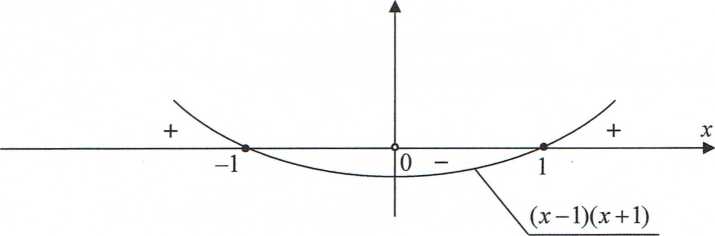
Wyszukiwarka
Podobne podstrony:
Wskaż m. dla którego funkcja liniowa określona wzorem /(x) = (;«-1)xt3 jest stała, (jp m =
83 (107) 164 Pręt Jest ściskany siłę S, która Jest równa reakcjom ścian. Po uwzględnianiu prawa Hook
262 IV. Badanie funkcji za pomocą pochodnych 4) Druga pochodna funkcji jc (w tym samym przedziale)
110,111 Epitet może określać cechę, która jest naturalną właściwością przedmiotu; tak dzieje się w p
Reguły deltaPrzykład: test na zero W wielu funkcjach konieczne jest sprawdzenie, czy liczba jest rów
397 S 2. Funkcje uwikłane 2) w punkcie tym funkcja F(x, y) jest równa zeru: F{x0, yo)=0; 3)
LICZBA DOSKONAŁA Liczba doskonała to taka liczba, która jest równa sumie wszystkich swoich dzielnikó
Weierstressa Twierdzenie Weierstrassa Funkcja ciągła i określona w przedziale domkniętym [a,b] jest
250 Hubert L. Oczkowski scencji (zwana resztkową) jest równa zeru. Dodatkowe badania struktury ceram
1 GR 1. 1 prawo Netwona (I) Ciało, na które nie działa żadna siła (lub gdy siła wypadkowa jest równa
skanuj0002 4 • indukcja jest równa zeru nie u osi poprzecznej, lecz, w punkcie prz
skanuj0005 Równowaga trwała występuje w punkcie x0gdyż nachylenie krzywej jest zerowe, wobec czego s
więcej podobnych podstron