0431

432

VI. Wyznaczniki funkcyjne i ich zastosowania

mujemy od razu

dy 1 d²y dx dx ’ dx²

7y

d²x

dy²

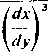
/d²x\² dx d³x d³y ^ \dy²) dy dy³ Tc³    7dx\*

W

dy d³y

Na przykład, jeżeli zastosujemy taką zamianę roli zmiennych w wyrażeniu W=— • —5 —3

,3    dx dx

d x

dy³

to nadamy mu postać fV~——-

[dx

\dy

4) Przejście do współrzędnych biegunowych. Jeżeli x, y rozpatruje się jako współrzędne prostokątne punktu na płaszczyźnie, to równanie y=f(x) przedstawia krzywą. Często wygodniej jest przejść do współrzędnych biegunowych r, 8 przedstawiając krzywą równaniem biegunowym r = g(0). Wówczas trzeba naturalnie różne wielkości geometryczne związane z tą krzywą i wyrażone za pomocą x, y,

dy d²y    dr    d²r

— , —-z, ... wyrazić za pomocą 0, r, -- ,    ₂ , ...

dx dx    do do

Wzory na przekształcenie mają w tym wypadku jak wiadomo postać ,r = rcos 8, y = rsin 0. Różniczkując je względem 8 i pamiętając przy tym, że r jest funkcją 8, otrzymujemy

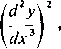
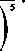
dx    dr    dy dr

—- =—cos0 — rsin0, -= —sin0 + rcos0,

dO    dd    dO dd

d²x    d²r    dr

—r =—= cos 8 — 2 — sin 0 - r cos 0, dt9²    d0²    dd

d²y    d²r    dr

—, = —rsin0+2 —cos0 — r sin&, ... d8²    d0²    d8

Teraz ze wzorów (2) pisząc w nich 0 zamiast t otrzymujemy

dr

de²

dr

—    sin0 + rcos0 ,

dy_d8    d²y_

dx dr    dx² [dr    \³

— cos0—rsin#    I—cos0 —rsin0

dd    \ dd    J

r² +2

Możemy teraz na przykład obliczyć współczynnik kierunkowy stycznej

dr

dy dd tga = — =

sin0+rcostf

dx dr

— cos 0 — r sin 0 dO

Tangens kąta co utworzonego przez styczną z przedłużeniem promienia wodzącego (rys. 114):

tgtu=tg(a—0) =

dy

x--y

tg a—tg 0    dx

1 +tgatg0    dy

x+y — dx