0463

464

VII. Zastosowania rachunku różniczkowego do geometrii

ma wyznaczniki

]2y Iz

|2y 0

-4 yz.

2z

0

2x

2 x-R

=4xz — 2Rz

2x

2 x-R

2 y 2 y

= 2 Ry,

które są równe zeru w tym punkcie.

Krzywą Vivianiego można przedstawić parametrycznie, np. w następujący sposób: je = Rsin²/,    y = Rsinrcosr,    z = Rcosf,

Istotnie, nietrudno jest sprawdzić, że te wyrażenia spełniają tożsamościowo równania uwikłane krzywej i że gdy parametr t zmienia się np. od 0 do 2tt, to punkt (x, y, z) opisuje całą krzywą. Punkt (R, 0, 0) otrzymujemy dwukrotnie: dla/=_Trr i / = jest to więc punkt podwójny, jak się tego zresztą należało spodziewać.

2) Są przypadki, w których przedstawienie parametryczne krzywej wynika w sposób naturalny z samego sposobu powstawania krzywej. Rozpatrzmy na przykład linię śrubową. Jej powstawanie można przedstawić w następujący spo

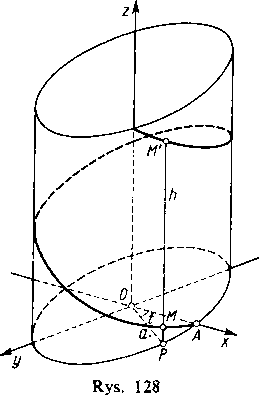
sób. Przypuśćmy, że pewien punkt M znajdujący się w chwili początkowej w A (rys. 128) obraca się jednostajnie dokoła osi z w kierunku zgodnym z ruchem wskazówek zegara i przy tym jednocześnie bierze udział w ruchu jednostajnym postępowym równolegle do osi z i zgodnie z jej zwrotem. Trajektoria punktu M nazywa się linią śrubową. Jako parametr określający położenie punktu M można przyjąć kąt t, który tworzy z osią x rzut OP odcinka OM. Współrzędne * i y punktu M i punktu P są takie same, zatem x = a cos t i y=a sin t, gdzie a jest promieniem okręgu opisywanego przez punkt P. Przesunięcie pionowe z rośnie proporcjonalnie do kąta obrotu t, bo obydwa ruchy — obrotowy i postępowy — są jednostajne. Zatem z=ct. Równania parametryczne linii śrubowej mają więc ostatecznie postać

(15)    x = acost, y = asinr,    z = ct.

Otrzymana linia śrubowa jest lewoskrętna, przy prawoskrętnym układzie współrzędnych te same równania określają linię śrubową prawoskrętną.

Łatwo jest wyrugować parametr r z równań (15); np. wyznaczając t z ostatniego równania i wstawiając w pierwsze dwa otrzymujemy

z    z

x — a cos —,    y = asin —.

c    c

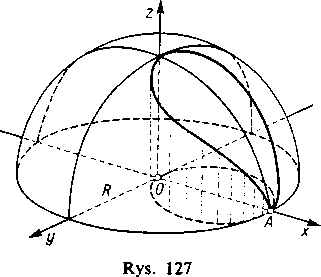
3) Rozpatrzmy sferę o promieniu R i środku w początku układu (rys. 129). Jej równaniem uwikłanym jest jak wiadomo

4 i 4 , i _nZ

x + y +z =R .