0517

518

VII. Zastosowania rachunku różniczkowego do geometrii

Podstawiając do wzoru (lOa) otrzymujemy po uproszczeniach

Z=x + 2x y , r/=y + ix y

Z równań tych łącznie z równaniami samej asteroidy można wyrugować x i y w następujący sposób: *_+ł = U^1,,+y^,,,)\    ć-t7=(*^1/3-/^/3)\

(i+ti)^2l3+(ę-’l)^2,3=2(x²¹³ +y^2l3)=2a¹³ .

Obróćmy osie układu o 45°. Nowe współrzędne fi, tu wyrażają się przez stare współrzędne <f, <7 w następujący sposób:

<£i

(+rj

*7i

V2"

W nowym układzie współrzędnych równanie rozpatrywanej ewoluty ma postać

«f³+7?^/3=(2«)^2/3.

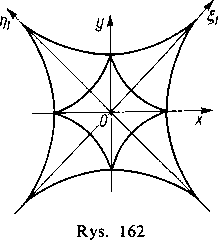
Poznajemy od razu, że jest to znowu równanie asteroidy. A więc ewolutą asteroidy jest także aste-roida tylko dwukrotnie większa i o osiach obróconych o kąt 45° względem starych osi (rys. 162). Przykład 4. Znaleźć ewolutę cykloidy x=a(t—sin f), y=a(l— cos f).

Ponieważ wiemy [231, 4)], że dla cykloidy jest

a=in—it,    da——\dt,

powstaje z niej przez

więc wygodniej jest posłużyć się wzorami (9). Podstawiając do nich powyższą wartość da otrzymujemy i=x+2y',,    tj=y-2x;,

czyli

Ć = a(t+sinr) ,    rj= — a(l — cosi) .

Przyjmując t = x—n napiszemy znalezione równanie parametryczne w następującej postaci:

Ć = — tta + a(r—sinr) , if= —2a + a( 1 —cosr).

Widać stąd, że ewolutą cykloidy jest cykloida przystająca do niej, ale przesunięta o odcinek na w lewo (równolegle do osi x i w stronę przeciwną do zwrotu psi) i o odcinek 2a w dół (równolegle do osi y i również w stronę przeciwną do zwrotu osi).

Pozostawiamy czytelnikowi przekonanie się o tym, że ewolutą epicykloidy i hipocykloidy jest także przystająca do wyjściowej krzywej zwykły obrót.

Przykład 5. Znaleźć ewolutę spirali logarytmicznej r—ae^m>.

Geometryczna konstrukcja środka krzywizny pokazana w ustępie 252, 5) pozwala z łatwością znaleźć jego współrzędne biegunowe r_t i 8i. Mianowicie (patrz rys. 134 na str. 471):

ri=/ip = rctgta = mr,    0,=0+ijr.

Rugując r i 0 z tych równań i z równania samej spirali otrzymujemy równanie ewoluty

ti = mae ¹    ~ai e ¹.

Obracając oś biegunową o odpowiedni kąt można utożsamić to równanie z równaniem wyjściowym. Tym samym ewolutą spirali hiperbolicznej jest taką, samą spiralą i otrzymuje się ją ze spirali wyjściowej przez obrót dokoła bieguna.

Konstrukcją ewolwent danej krzywej zajmiemy się później gdy zbadąmy pewne własności ewolut i ewolwent.