092

92

6. Testowanie hipotez

m= 1.8. Natomiast hipotezę, że m = 1.5 należy przy tym samym poziomie istotności już odrzucić na korzyść hipotezy m > 1.5, gdyż wtedy t_oh = 6.35.

Uwaga. Ponieważ zmienna losowa t jest oznaczana zgodnie z tradycją, małą literą, to dla odróżnienia zmiennej losowej t od jej wartości f(o>), będziemy wartość statystyki r(a>) oznaczać przez ^łobs’ (jako wartość obserwowaną). Tę samą uwagę zastosujemy do zmiennej losowej £², statystyki F omawianej w punkcie 6.1.4 oraz statystyki X omawianej w punkcie 6.2.1.

6.1.2. Testy dla wariancji

Przy testowaniu hipotezy dla wariancji H₀: a = <J₀ będziemy brać pod uwagę tylko jedną hipotezę alternatywną H_{ : a > a₀. Do testowania takiej hipotezy używana jest statystyka

(n -1 )Ś²

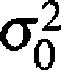
(6.1.4)

Jeśli cecha w populacji generalnej ma rozkład normalny, to statystyka (6.1.4), obliczona z próby n-elementowej, ma rozkład chi-kwadrat on~l stopniach swobody. Z tablic odczytujemy wartość %a taką, że Pr(^² > Xa) ⁼ Je-żeli Xohs ^> %a> to odrzucamy hipotezę, że <7 = a₀ i przyjmujemy hipotezę alternatywną cr>tJ₀.

Przykład. Dokonano 10 pomiarów pewnej wielkości i otrzymano wyniki: 4.98, 4.92, 4.88, 4.98, 5.02, 4.99, 5.08, 5.03, 4.86, 4.93. (Dane te pochodzą z próby o rozkładzie N(5,0.1)). Sprawdzić, że pomiarów dokonano przyrządem o dokładności nie gorszej niż 0.05.

Dokonamy tego stawiając hipotezę zerową H₀ : a — 0.05 przeciw hipotezie alternatywnej : <7 > 0.05. Przyjmiemy poziom istotności a = 0.05.

Obliczając momenty empiryczne otrzymujemy s² = 0.004779 oraz s = 0.06913. Stąd i ze wzoru (6.1.4) mamy %l_hs = 17.20. Ponieważ dla 9 stopni swobody mamy %²t = 16.919, więc odrzucamy hipotezę zerową na korzyść alternatywnej, czyli przyjmujemy, że dokładność jest gorsza niż 0.05. Jeżeli jednak zadowala nas dokładność 0.1, to wtedy %²hs = 4.30 i stwierdzamy, że nie ma podstaw do odrzucenia takiej hipotezy.

Jeżeli n jest duże, to statystyka x² określona wzorem (6.1.4) ma rozkład asymptotycznie normalny N(n— 1, y/2(n — 1). Dlatego zamiast statystyki (6.1.4) wygodniej użyć statystyki

(6.1.5)

_Tt_

72(^T) ’

o rozkładzie w przybliżeniu N(0,1).