116 117 (4)

116

Przestrzenie euklidesowe

3 (o-i, y) = 3 (crii) y: — 2(ati) yz — 2 (az₂)y, + 4 {ctx₂)y₂ = a (3i| yi - 2xiy₂ - 2x₂y\ + 4r₂y₂)

=

Sprawdzamy warunek 4. Mamy (5, i) = 3zJ — 4rir2-Mx²- Jest to trójmian kwadratowy zmiennej r;, dla którego A = — 32 (z2)² ^ 0. Stąd wynika, że (z x) ^ 0. Warunek 5. jest także spełniony, bowiem oczywiście (O d) = 0 Jeżeli natomiast (i x) = 0, to rozważany poprzednio trójmian kwadratowy ma pierwiastek i A = 0. Stąd z₂ — 0 oraz Z] = 0, zatem i — 0.

b) Niech p, q r E /Zi[x] oraz a € R. Podobnie jak poprzednio mamy

1 (P. <7) - P(O«(1) + 2j>(2)0(2)= g(l)p(l) + 2₉(2)p(2) = (g,p)

2- (p + q, r) = (p(l) + q{ 1)) r(l) + 2(p(2) -f g(2)) r(2)

= (p(])r(l) + 2p(2)r(2)) + (g(l)r(l) + 2g(2)r(2))

= (P.    +    r),

2- (ap, ę) = (op(l))ę(l) + 2(orp(2)) ^(2) =ar(p(l)7(l) + 2p(2)ę(2))

= a(p. g),

4    (p,p) = p²(l) + 2p²(2)>0,

5    (5, 0) = 0, a 2 warunku (p, p) = 0 wynika żc p(l) = p(2) = 0.

Funkcja p jest wielomianem stopnia 1 lub funkcją stałą. Zerowanie się tej funkcji w punktach z = 1 i r = 2 oznacza, żc p(x) = 0.

Przykład 12.2

Uzasadnić, ze podane funkcje (*,•) nie są iloczynami skalarnymi we wskazanych przestrzeniach liniowych:

'213'		yi
-i 1 0		V2
3 0 1		L V3 .

a) (5, y) = 5xiy, - 3x_:y₂ - 3z₂yi + yW2 dla x = i>i,r₂), y = (yi,y₂) € li²; ^b; (*, y) = |ri x₂ x₃)

dla x = (zi,i₂,r₃) y = (yi _:y₂,y₃) 6 li³; O (p. gj = p(0)g(0) + p(l}g(l) dla p,qe Jt₂[*].

Rozwiązanie

a)    Funkcja (-,•) nie spełnia warunku 4. (patrz rozwiązanie Przykładu 12.1) definicji iloczynu sxalarnego. Traktując bowiem wyrażenie (i, z) = 5xJ -6zj z₂ + z\ jako trójmian kwadratowy zmiennej ii otrzymujemy związek A = 16z² ^ 0. Możliwa jest więc sytuacja, że (5, z) < 0 np. dla i = f-.l). Dodatkowo można jeszcze zauważyć, że istnieje

niezerowy w-cktor, np i = (1,1), dla którego (x, i) = 0. To oznacza, że również warunek 5. definicji iloczynu skalarnego nie jest spełniony.

b)    W tym przykładzie warunek 1. definicji iloczynu skalarnego nie jest spełniony. Macierz

definiująca funkcję (*,*) nie jest symetryczna i łatwo wskazać dwa wektory, np. x = (1,0,0), y ~ (0,1,0), dla których [x, y) = 1    -1 = (y, 5).

c.) Załóżmy, że dla pewnego wielomianu p € fi₂[z] zachodzi związek (p. p) = o. To oznacza, że p²(0) + p²(1) = 0, a zatem p(0) = p(l) = 0. Łatwo wskazać niezerowy

Dwunasty tydzień - pizykłady    117

wielomian p słupnia ^ 2 spełniający otrzymaną zależność, np. p(x) = x(x — 1). Warunek 5. definicji iloczynu skalarnego me jest więc spełniony

• Przykład 12.3

W przestrzeni euklidesowoj E⁴ :

a)    obliczyć, normę wektora (1,-2,3,—4);

b)    zbadać ortcgonalność wektorów (2, —3,1, —1), (6.1, —2,7);

c)    obliczyć kąt miedzy wektorami (1,2,1,—2), (—2,1 0,1);

d)    znaleźć wszystkie wektory ortogonalne do wektora (1,0,1,0) i wskazać jeden taki wektor o normie równej 3;

e)    podać przykład wektora unormowanego tworzącego z wektorem (1,1.—1,0)

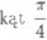
Rozwiązanie

a) Niech z = (1, — 2, 3, — 4). Wówczas

|*| = v^/(i,ź) = \/l* + (-2)’ + 3² + (—4)² = >/3Q.

b)    Oznaczmy podane wekLory odpowiednio przez X, y. Mamy (z, y) = 0. zatem wektory te są ortogonalne.

c)    Dla podanych wektorów i, y mamy

cos (z, y) =

(g.y) ₌

1*1 liżl vi()\/G

V15

15

czyli $ (z, y) = arccos |    J

d) Dowolny wektor z = (a,b,c,d) € E* ortogonalny dodanego wektora y spełnia związek (z, y) = u + c = 0. Stąd wynika, że z = (c b, -a. d), gdzie a, b, d £ R Wszystkie wektory o tej własności tworzą więc przestrzeń liniową lin {(1,0, -1, 0), (0,1,0, 0), (0, 0,0.1)}. Wektor o normie równej 3 należący do tej przestrzeni spełnia dodatkowo warunek 2a² ■+-b² 4 d⁷ = 9. Przykładem takiego wektora jest Zj = (2,1,—2,0).

c) Niech z = (a,b,c,d) będzie szukanym wektorem, y = (1,1,—1,0). Wówczas mamy a² 4- b* + c² + d^A = 1 oraz

cos $ (z, 5) =

a + b — c

7T~

2

Stąd wynika, że a + b — c =

— -\/6, zaś d = y/1 — a? — fc² 4

i\/6. Przykładowo można przyjąć, że a = 6 = i\/6, c =

2    o

= ^\/7 Ostatecznie z = ( i\/6, ^n/6,— -V6,    •

• Przykład 12.4

Obliczyć kąty między wektorami p₀ = 2 — 4x, ę₀ = z - 2 w przestrzeni euklideso-wej 12i[x] z podanymi iloczynami skalarnymi: