121

Analizo statystyczna pomiarów 121

m2 =

4.0800 5.0600 5.3200 4.6800

Odchylenie standardowe std

Odchylenie standardowe s zmiennej .t jest obliczane za pomocą funkcji std(x). W wyniku otrzymuje się wektor wierszowy zawierający odchylenia standardowe danych w poszczególnych kolumnach macierzy x

s = [.v,    ,v_:    ... .9, Sj ... ,v„ ].    (10.4)

Odchylenie standardowe .s, jest liczone zgodnie z następującym wzorem

-m,)²

(10.5)

w którym N oznacza liczbę elementów w kolumnie.

W przypadku przykładowej macierzy x wywołanie funkcji std() daje następujący wynik:

s=std(x) s =

2.5184    0.5965    1.8839    1.0954    1.1804

Odchylenie standardowe liczone według wzoru (10.5) jest odniesione do /V- 1 elementów. Niekiedy jednak użytkownik jest zainteresowany odniesieniem odchylenia standardowego do N elementów, zgodnie z następującym wzorem

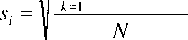
(10.6)

W nowszych wersjach Matlaba możliwe jest zastosowanie wzoru (10.6) zamiast (10.5) przez wywołanie funkcji std() z parametrem flag. Parametr flag = 0 odnosi się do wzoru z N - 1 , zaś flag = 1 - do wzoru z N.

Możliwe jest również wskazanie wymiaru, wzdłuż którego obliczane jest odchylenie standardowe.

W przypadku przykładowej macierzy x kolejne wywołania funkcji std() dają następujące wyniki: