127

Analiza statystyczna pomiarów 127

Normalny rozkład prawdopodobieństwa

Najczęściej w analizie statystycznej pomiarów wielkości elektrycznych mamy do czynienia z rozkładem normalnym prawdopodobieństwa.

Funkcja prawdopodobieństwa rozkładu normalnego to tzw. krzywa Gaussa opisana wzorem

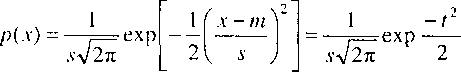
(10.11)

w którym:

m

s

-    wartość oczekiwana,

-    odchylenie standardowe, t - {x - m)/s - zmienna losowa standaryzowana.

W celu zobrazowania krzywej Gaussa na wykresie opracowano funkcje rngaussO oraz rnrys().

Funkcja rngaussO oblicza gęstość prawdopodobieństwa i ma następującą postać:

function gp=rngauss(x,m,s)

% krzywa Gausssa

% gp(x)=1/(s*sqrt(2*pi))*exp(-((x-m)/(sqrt(2)*s))~2)

Im- wartość średnia, s - odchylenie standardowe % gp - gestosc prawdopodobiensta p2pi=sqrt(2*pi); p2=sqrt(2);

% standaryzacja zmiennej losowej

t= (x-m)/(p2*s) ;gp = 1/p2pi*exp(-1.^2) ;

return

Funkcja rnrysO rysuje krzywe Gaussa w przedziale m - 3s <= x <= m + 3.v, dla zadanej wartości średniej m i zmieniających się odchyleń standardowych s.

function rnrys

% graficzny obraz rozkładu normalnego m=3;

x=0:0.02 *m:2 *m;

S = 0.1 : 0.1:1 ;

ns=length(s) ; for k=l:ns

y=rngaussa(x,m,s(k)); p 1 o t (x, y, ' r ' ) ;

if k==l hołd on; end

end

grid on;

xlabel('x'); ylabel('N(x,m,s)');