146

ej

Granica funkcji

R - 0}. 0 G D^d, a więc gdzie x_n = 1/mr,

:raz x_n ± 0, y_n ^ 0 dla

Zatem

lim(l + x)^l^^x = e.

x—>0

Przykład 14.5_

Nietrudno wykazać (na podstawie przykładu 14.4), że

lim (l + -) =e, lim (l + i) = e.

x-*+oo y x)    x-^-cx) y x)

Przykład 14.6

Korzystając z przykładu 14.4, mamy

ln(l + t)    1 .    . , /_.    _x

lim-= lim — m(l + x) = lim ln(l + x)

x—>0    X    x—>0 x    x—>0

1 fx

= lne = 1.

Przykład 14.7 Rozważmy granicę

■—>’^ch. granic, więc -

x—>0    X

Niech e^x — 1 = t. Stąd e^x = 1 + £, więc lne^x = ln(l4-t), i dalej x = ln(l 4-i). Ponadto

x —* 0 ■<=>■ t —> 0.

Zatem mamy

lim -= lim -—₇-- = lim ;    ^ .

*-+0 X    ^0ln(l + t)

Ostatnia granica jest równa 1 na podstawie przykładu 14.6.

Niech teraz /: D —> R oraz niech t₀ G D^d. Załóżmy dodatkowo, że x₀ jest lewostronnym (prawostronnym) punktem skupienia zbioru D.

ZA jważyć, że (—1,0) U i'Ze^: granicy ma sens. = 0 (i {z_n} C D_f "• tedy, korzystając

Definicja 14.2. Jeżeli dla każdego ciągu {x_n} c D takiego, że x_n —> x₀ oraz x_n < .T₀ (x_n > t₀, dla n = 1,2,...), ciąg {/(T_n)} jest zbieżny do tej samej granicy g. to g nazywamy granicą lewostronną (prawostronną) funkcji / w punkcie t₀ i oznaczamy

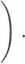
lim f(x) j lim f(x)

x—*xq    yx-x+

151