2011 12 19";52;522

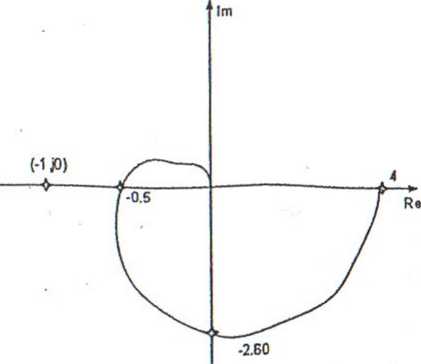
Czyli przecięcie osi Re Jest w punkcie (-0.5, JO), a więc wykres nie obejmuje punktu (-1,J0). Z powyższych warunków wynika, że układ zamknięty jest stabilny.

Zapas fazy

= >

G{jw) =

4

(jw+l)³

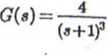
|G(*»)l = -7=4=r-B-JL_

(v/w2+l ż)5

zapas fazy liczymy dla modułu równego 1, więc:

= >

(yfJ+\f    (^2+1)9 = ₄    __>    (w2 + 1)3 ₌ 16

=> w = ±\fe/l6Si

' to Jest oj dla której moduł wynosi 1.

A0 = ISO” - 3arctan(w) = 27.1°

Zapas wzmocnienia

"-jK-²

b) Korektor szeregom Korektor szeregowy ma ogólną postać: .T*a+1

AjT-

2^+1

- wyznaczanie A

Transmltancja układu z korektorem:

<?„(*) = -

.Th+1

4/ir*ji+4A

s3+3*2+3s+l    ^₊₁    (,3+3*2+33₊i)(™_a+i)

Uchyb układu z korektorem:

£«=

frfr) _|_.

1+G₀(e)    ! | 4AT_t3+U

(«3+3<rf+3<4-l)(—«+l)

(s3+3s2+3s+l)(^s+l)

* (s3+3s2+3*+l)(^s+l)4-4ylT^+4yi Uchyb ustalony układu z korektorem:

E„(a)= Im^sE(s) = lim sj ■

(s3 + Hjfl 4* 3a+l)(4jr^+1)

(s*+3a J+3j+1)    +1)+ 4yt?V+iA

1

4y4+l

=Ł=>

Jeśli uchyb ustalony ma być równy 0.05, to: 4A+1    20

A“19/4

wyznaczanie Q