2011 12 19";53;593

j(3w-w3)    3w-w»

2) Im[G(ju)] = O

3(j—w³ = 0 w — |_ub cj = 0

RelGU^OU^jĄzi

-1.85

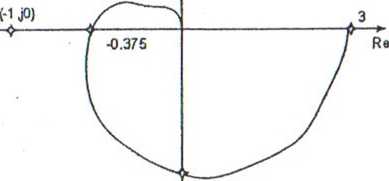
Czyli przecięcie osi Re Jest w punkcie (-3/8, JO), a więc wykres nie obejmuje punktu (-l,jO).

iMG(jw)) = -f _jub ^[0(^ = 3

Robimy tabelkę:

CO	0	V3/3	V3
Re[G(Jo>)]	0	3	-0.375
Im[G(ju>)]	-1.95	0	0

Im

Z powyższych warunków wynika, że układ zamknięty jest stabilny.

Zaoas wzmocnienia

^al=i?=ł=l“²⁶⁶⁷

8

yj Zadanie 5

Zadanie;

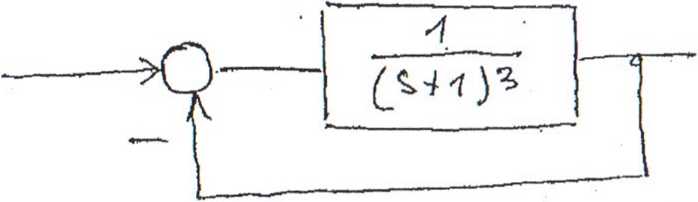
Obliczyć uchyb ustalony położenia układu jak na rysunku. Jeśli błąd ten jest większy od 0.1 (10%) to zastosować korektor szeregowy, który obniży ten błąd do tej wartości.

Rozwiązanie:

Obliczenie uchybu ustalonego 1 1

E(s) =

(a+l)³ as + 3sż+3j+l

^Ul³) _ i _ 1 *i-(-3s8Z + 3j+1 l+C?o(s) i_j--1- ³ «³+3aż4-3a+2

»3+3/!+3s+l

E_u(a) = lim aE{s) = lim    = -

«-*0 ^v '    «->D ‘ aJ+3aż+3a+2    2

bLflbllczenle korektora szeregowego Korektor szeregowy ma ogólną postać:

3