22

40
Ogólny błąd poprawek wynosi:
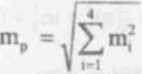
oraz przedział błędu:
1.0’ ś mp <; 2?
0,9* £ nip £ l\ gdy mierzono obniżenie widnokręgu Ogólny błąd wysokości obserwowanej (h,,) oznaczono symbolem m. I
W dalszej części (rozdz. 3) w wartości m wyróżnia się dwa składniki: e i o - wartości błędów przypadkowych i syste-: matycznych. Mówiąc ogólnie o błędach pomiarów lub obliczając I wskaźniki dokładności serii pomiarów należy stwierdzić, że j składnika błędu systematycznego nie da się określić. Wszelkie' oceny oparte na rozkładzie normalnym mogą mieć uzasadnienie wówczas, gdy składnik o jest nieznaczny i występuje jednocześnie w kilku różnych źródłach o charakterze losowym. Ogólny błąd obliczony z poszczególnych składników wynosi:
±l,2'£iHk £2,5* (2.10)
o
Doświadczenia własne autora z ostatnich lat wskazują, ze lak określony przedział błędu jest raczej przedziałem błędów największych. Uwzględniając dokładniej panujące warunki pomiaru i zasady metodyki można uzyskać wyniki obarczone błędem połowy wartości (2.10) dolnej granicy przedziału. Można także inaczej oceniać składowe błędu wysokości obserwowanej, analizując z osobna każdą wartość występującą w poprawkach i samym pomiarze wysokości. Pomiar wysokości charakteryzuje się błędem m o wartościach: ±0,5* dla Słońca. ±0,8’ dla gwiazd i planet. Są to jednak wartości błędów przypadkowych. Błędy systematyczne (7) pochodzące od nachylenia sekstantu przy dużej wysokości wynoszą od 0 do 3\ błąd osobniczy - do 0,2’. Błąd systematyczny pomiaru iuuI horyzontem nocy księżycowej, zależny od różnicy azymutu Księżyca i obserwowanej gwiazdy, zmienia się w granicach od +1' do -2'. Możliwe też są błędy systematyczne nieuwzględniania błędu stałego (s) sięgające od ±0,5' do ±1't dla starych sekstantów. Obniżenie widnokręgu może wnosić błąd systematyczny < \\ w skrajnych przypadkach nawet 2' do 3*. Błędy wpływu refrakcji i paralaksy. szczególnie przy małych wysokościach Słońca i Księżyca, mogą dochodzić do ±0,3'. Wartości błędów systematycznych w konkretnych obserwacjach mogą być ujawnione i wyeliminowane tylko po obserwacjach i opracowaniu Wstępnie może być jedynie określony rząd wielkości błędu systematycznego. Wartości błędów przypadkowych lub też ogólnych oszacowane /ostały powyżej wartościami błędów średnich (standardowych).
Błąd przypadkowy uwidacznia się rozproszeniem wyników pomiarów wykonywanych w zasadzie w nie zmienionych warunkach. Wartości błędów w poszczególnych pomiarach nie da się przewidzieć, jedynie można rozpatrywać takie prawdopodobieństwo. Zwykle określa się przedział błędu i prawdopodobieństwo wy stąpienia wartości w danym przedziale:
p(|x|<;m)= <rKl)- 4>(-l) = 2<t>(l) = 0,683
w którym:
<t> - funkcja Laplacc'a, wartość wybierana z tablicy.
ł*rawdopodobieństwo pojawienia się wartości błędu przypadkowego w przedziale ±m wynosi 68,3%. Wielokrotności (podwielokrot-ności) przedziału błędu standardowego charakteryzują się następującym prawdopodobieństwem:
|
0,674 m |
m |
1.96 m |
2 m |
2.58 m |
3 m | |
|
p |
50% |
68.3% |
95% |
95,4% |
99% |
99.7% |
Wyszukiwarka
Podobne podstrony:
40 Ogólny błąd poprawek wynosi: oraz przedział błędu:1,0’ ś nip S 2J 0,9* ś nip £ \ gdy mierzono
img163 163 przedziale jego zmienności jest jednostajny, średniokwadratowy błąd kwantowania wynosi za
262 R. Strojny, R. Piotrowski Błąd względny zawiera się w przedziale 0,2-8,7%. Średni błąd wynosi 3,
Scan Pic0266 40 4. Funkcja 10+lg tg* oraz lO+lgctg* x dla lgtgx 0 1 2 3 4 5 Poprawki dla 1&
poprawnosc jezykowa imiesłowy równowaznikowe zdań 2 V. Proszę wskazać zdania błędne, poprawić je o
IMAG0465 dla Ux = 1 V Zadanie 11 Dany jest woltomierz cyfrowy o zakresie 1,0000 V, którego błąd pods
img052 52 Ka przykład, dla = +20°C» T = 10°C i długości linii 100 u poprawka wynosi około -12 no. da
img131 131 M [16] pokazano, jak w ogólny* przypadku należy dobierać koóce przedziałów kwantowania
img133 133 • odstęp sygnał - błąd kwantowania 133 q (1.4.lOb) Hielkość błędu kwantowania
img139 139 Odstęp sygnał - błąd kwantowania wynosiłby wtedy (1.4.15) i byłby niezależny od poziomu s
więcej podobnych podstron