algebra5str2

5. Dla pewnych liczb a, b, c, d, e i / mamy det

	' a 3 c
det	6 5 e c 7 ,f
Z tiJAćh*J'^/>0'> c.
cWj	o- 3 <^] t 3 e C 3 # J

a 1 dl	‘a 1 dl	■ a 3 d
ó 1 e = 17 i det ■ 1 fi	i 2 e = 11. Wyznaczyć det m^3 fi	b 3 e — /J	|

. Przedstawić uzasadnienie swojego rozumowania

lf A fe A €

<■ " ł

jl

j-3-175F7

U[ff f]'    ^f ~&-{2^)okt[c /J +    <bj ~

- -2    [?u* ^fti!JIMft:^{]-1 <&[??]⁺1 Mtfj

“ *11/ **Hf uJ • L^r*:]=

^Jll

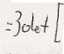
Z-^+17 =33

6. Sprawdzić, czy zbiór i2+ * {a: €    : a; > 0} z dodawaniem © i mnożeniem ©, gdzie x (& y = xy i r ę> x = x^r dla x,y € R+ ¹

r € ft, jest przestrzenią wektorową? Uzasadnić swoją odpowiedź.

3 x*3rX V A ~s\    P^a

— 1 [/''"*'||| £>* f rz.*)h2_asJX

i

O    " KiASdg&9! Wm §H

' i*p l^rs*y^&*

Jó MBM ^Z^*^^r ^    ■ I• i*n)-■■€ /2ⁿ: |xcif. = . . . = |rc_n)} jest podprzestrzenią wektorową przestrzeni i2ⁿ-

Si y WSI I-

f WS    |    • o 1

pi

vó^Pr a, 1’    f(^x'y»2) €/2³:x + j/ + _{2 =} o} jest podprzestrzenią wektorową przestrzeni /l³.

^ 5C3,-?,-V ^5^1*0 *>±±0    i°u^4,z>&S:x^r.u /i*4*

*-«*>- - O

'X,

-<*(xsy+z)-oc-0~0    ;o g<» t5

trzem

•^prawdzie. czy wektor x-_(l, ₂, _I)M kombl^i^ _wektorów _ _Xl , ₍₁, _LJ^ (1,1,2), xa= (0,1, fw p-

^HK

©<x»    ?

m

•ć + p¹ -1

MB

*c⁺2?»+jfW

1 -7 O 11 ^ 4 -7 b tj 2 i ^u«

jp$

H

* S) O

0 0 /f

mim

wm hxoh-

* 1Wmmm

joo i u.

Mm

"1 oo\Z

0 >) o ~1

0 0 -7 I

*> y?--ł

UOjfoy X

osii^T&rfotj j yj t ^,

■

H

SI

m