BEZNA~33

Rozwiązanie. Warunki początkowe

<l(0)

E

Ri+R ’

«c(0) =

R

R, + R

E

Po otwarciu łącznika W obwód przyjmuje postać jak na rys. 8.26b i można go opisać następującymi równaniami:

L^- +Ri_L-u_c = 0

-C

'l = »C =

Po przekształceniach otrzymujemy postać normalną równań stanu

duc

dt

		R 1 '
		L L		*Ł
	—	1
		i 0 |o 1 _i		«C

którego rozwiązaniem jest x = e^A'x₀

(a) Po podstawieniu wartości liczbowych otrzymujemy

i,.(0) = 2 A ;    «_c(0) = 4 V ; x₀ =

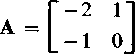
Z równania charakterystycznego

g (A) = det (A 1—A)

A+2

1

A²+2A + 1 = 0

obliczamy wartości własne macierzy A

Xi — A₂ — A — — 1

Stosujemy rozwinięcie funkcji macierzy e^A' w szereg skończony e^A< = oc₀ 1 + A

i korzystamy z twierdzenia Cayleya-Hamiltona, zgodnie z którym funkcja macierzy f (A) musi być spełniona przez wartości własne

e^2f = ao + otj A

Ponieważ wartości własne są jednakowe, tzn. Aj = A₂, zatem równanie to należy zróżniczkować stronami względem A

t e^-t = oc_t

231