BEZNA~39

Stąd

a₀ = e^_‘(0,5 sin 2ć + cos 2t) cc_t = 0,5e^_‘sin 2t

e

Al

a₀ 1+aj A =

e ‘cos 21 0,5e^_‘sin 21

—2e 'sin 2t e^-‘cos 2t

Ponieważ wymuszenia w obwodzie są niezależne od czasu, zatem

J e^A(,-rJBu dt = e^Al J e ^ArBu di = e^A,( —e ^At)|* A^-1Bo =

-A/'

A/

= e^A,(l —e^_A') A"‘Bu = (e^-ljA^Bu

=fl. —K jg

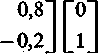
r _Xa__T)    I^-e^_‘cos 2t-l — 2e~‘sin 2fj T — 0,:

Je Budź j_o,5e^-tsin 2t e^_‘cos2f—lj 0,:

T0,8e“‘cos 2t+0,4e"‘sin 2t—0,81 ^— |_0,4e~‘sin 2t—0,2e"‘cos 2/+0.2J

Ostatecznie

f e ‘cos 21    —2e ‘sin 2tl R),8e ‘cos 2f+0,4e ‘sin 2f—0,81

|_0,5e^-‘sin 2f    e~‘cos21 J ⁺ |_0,4e^-‘sin 2f-0,2e^_‘cos2t+0,2j

r2e"‘cos 2t—4e"‘sin 2f—0,81 |_ e ~ ‘sin 2t+2e “ ‘cos 2f+0,2J

W chwili t = *i następuje otwarcie W2 i rozpoczyna się nowy stan nieustalony, dla którego warunki początkowe są określone przez wektor

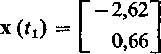
Stan nieustalony dla t > ^

Dla t ^ t₁ obwód ma postać jak na rys. 8.29c, a opisujące obwód równanie stanu jest następujące:

R 1

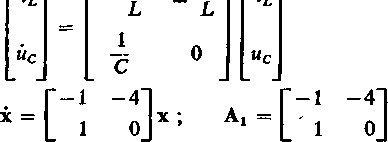
Rozwiązanie tego równania ma postać x = e^A‘^fx (fi)

237